Definitions in RCTs with interference

On May 25, I attended a workshop organized by the Harvard School of Public Health, titled “Causal Inference with Highly Dependent Data in Communicable Diseases Research.” I got to meet many of the “who’s who” of this literature from the fields of biostatistics, public health, and political science, among whom was Elizabeth Halloran, who co-authored this paper with Michael Hudgens – one of the more influential papers in the field.

While having a nice chat with her, we came to the realization that our work, which is geared more towards economists designing RCTs, and theirs addressing an audience more likely to be designing infectious disease trials define a lot of the same objects of interest, but give them different names. Since either paper is not the easiest read for a lay person interested in RCT design in the presence of interference (or highly dependent data or spillover effects), I thought it’d be useful to summarize these objects of interest and contrast what they’re called in Hudgens and Halloran (2008) vs. Baird et al. (2015) and talk about some of the more interesting concepts.

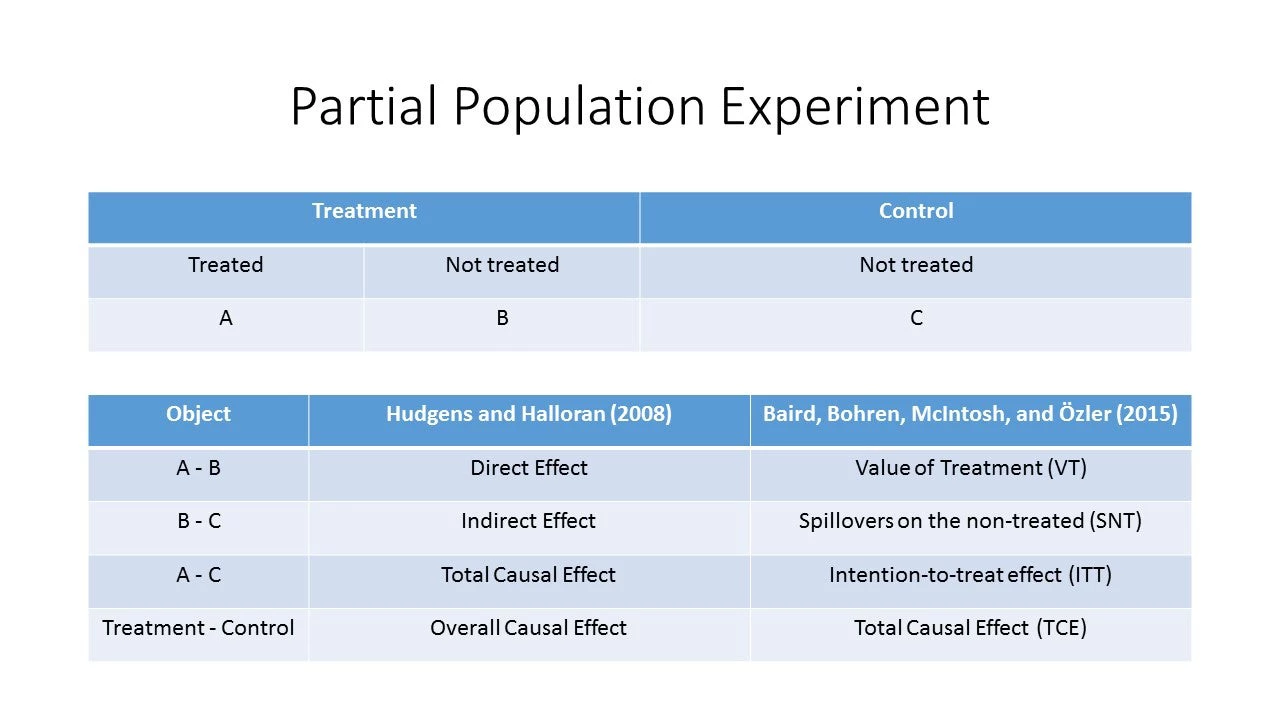
The figure below depicts a partial population experiment, where first clusters are assigned to treatment or control and then a certain proportion of the target population is assigned to treatment in treatment clusters. Hudgens and Halloran (HH) is more general than this (rather than control clusters with no treatment, there are clusters with another assignment mechanism: say, 75% treated in some vs. 50% in others), but assuming “pure control” clusters makes the comparison of concepts simpler for presentational purposes.



The first thing you’ll notice is that what HH call a “direct effect” isn’t even something that many economists would consider estimating unless they were convinced that spillovers were negligible to non-existent: otherwise you have a biased estimate of the intention-to-treat (ITT) effect. To see this, note that the “direct effect” under HH can be written as (A-C) – (B-C) = ITT – SNT, meaning that the direct effect is only equal to the ITT when there are no spillover effects within clusters.

We, however, decided to give this object a different name, Value of Treatment (VT), because it does have a meaningful interpretation: you can think of the “direct effect” or VT as the “individual value of receiving treatment in the treated cluster.” Think of it this way: the value of getting a, say, measles vaccination to you individually is very high if many people around you are not vaccinated but quite low if almost everyone is. In the latter case VT is close to zero, so if there is any cost to vaccination, you’d be more likely to opt out: bed nets may be a similar example. In contrast, you can think of deworming treatment, which has positive externalities for everyone: ironically, VT is close to zero at whatever share of the cluster is offered treatment – even though deworming can be very effective in the longer run if applied universally. Figure 1 in Baird et al. (2015) discussed such cases in more detail.
 
A couple of other interesting things:

1. the derivative of the TCE with respect to the share of the target population offered treatment shows that the policymaker’s decision to offer the treatment to one more person in a cluster is the sum of the individual benefit to that person, or VT, and the marginal social value, i.e. the spillovers from that person to others in the cluster – treated or untreated. If treatment is individually beneficial and the spillovers are positive, we want to treat more people. If the marginal spillovers are negative, the answer will depend on the relative size of VT vs. spillovers at that saturation.
2. Speaking of spillovers on treated and untreated individuals in treatment clusters, it’s important to note that the ITT can be decomposed into two components: what would the ITT effect be if only one person in each treatment cluster was randomly selected to receive treatment (and no one else)? We term this the “treatment effect on the uniquely treated” or TUT. The difference between ITT at any other saturation π, and the TUT is then the spillover effect on the treated, or ST(π) = ITT(π) – TUT. Believe it or not, you can run an experiment like this, as was done in Sinclair, McConnell, and Green (2012), who assigned only one household in some zip codes (clusters) to treatment in a large voter-mobilization experiment in Chicago, to identify the TUT. Alternatively, as described in our paper, you can assign clusters to a sufficiently large number of saturations, say 10% … 90% and extrapolate the ITT to ITT(1/n), making a functional form assumption. This is, by definition, less accurate, but it’s hard to think of many interventions where it is practical and cost-effective to assign clusters with one treated individual…

In the upcoming weeks, I’ll describe the main contribution of Baird et al., which has more to do with power calculations and optimal assignment of clusters into different groups rather than the objects of interest that I discussed in this post. Until then, I leave you with this poster that we had prepared for the workshop: