Last week I attended the
International Development Conference at the Kennedy School of Government, joining a session on social protection. The conference is organized by KSG students (kudos to the students for their hard work in making it happen and interesting!), and has a format with no presentations and informal panel discussions with invited speakers.
I happened to attend a session titled ‘ Big data for development: promises and perils’ that offered a lot of food for thought on privacy, confidentiality, digital rights, and data depository. Two fascinating points of discussion caught my attention. First, that the massive data available electronically in a myriad of forms provides a wealth of network of interactions. The field of computational social science is emerging to collect and analyze electronic data with an ‘unprecedented breadth and depth and scale’ and model economic and social interactions (see this article on Science here). This first point is first order and deserves its own space and attention.
The second point was made by Alex ‘Sandy’ Petland (the director of MIT’s Human Dynamics Laboratory and the MIT Media Lab Entrepreneurship Program among other things) who commented on the link between big data and inference. Paraphrasing the discussion: “With a large set of variables from different data sources, you generate lots of correlations. Some of these correlations might be the key to the missing key variables in a given context that small RCT studies with a limited number of controls might not provide (read omitted variable bias). You need to look at the structure of the data to make valid inferences’. This ‘big’ second question is the topic of this blog, spanning the debates already touched upon by this blog on external validity ( here), and the bigger questions of linking reduced forms to structural parameters.
How can we move beyond correlations in the presence of high dimensional data, and look for meaningful correlations and make valid inferences? A recent JEP paper by Belloni, Chernozhurov and Hansen reviews how the latest innovations in ‘data mining’ and how it links to causal inference and model selection. The paper follows and complements an outstanding mini-course online with the key recent econometrics developments, with publicly available videos and slides.
First of all what is big data? High dimensional data occurs when both ‘n’ (sample size) as well as ‘p’ (the number of available variables) are large.
The key objective of the empirical methods is to reduce this large dimension to a manageable set of variables (or what is referred to as ‘dimension reduction’). But how to parse the high dimensional forest and pick the important trees?
Prediction inference meets causal inference: both inferences share a common goal, reducing the dimensionality of high dimensional data to a manageable subset of variables with the objectives of 1) relating it to structural parameters of interest (causal inference) 2) making predictions (prediction inference).
Good data mining is a method that helps with this dimension reduction and model selection. The key for these specification searches is to find a rigorous method to do so. A popular method (LASSO) does so by minimizing squared errors, while putting a penalty on the size of the model (captured by the sum of absolute values of coefficients). LASSO and related methods are used to estimate these parsimonious models in an ‘approximately sparse’ way, that is by cutting irrelevant enough information while allowing some room for an approximation error. Potentially useful applications range from predicting regression functions to selecting instruments or controls.
What about causal inference? Take the problem of estimating treatment effects in partial linear models. Suppose to have your outcome equation:
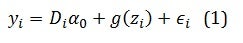
Where D the policy of interest, alpha is the impact.
The selection equation or auxiliary regression is given by:

where g(zi) and m(zi). and z is are the set of potential confounding factors (a linear function of controls xi or a polynomial transformation of xi). vi and Ei are error terms, (2) introduces the scope for omitted variable bias.
Belloni, Chernozhurov and Hansen propose a post double selection method:
This blog just scratches the surface of this nascent and important literature. The authors have already provided extensions to more general models, such as heterogeneous treatment effects and quantile treatment effects.
Time to retool. And I look forward to reading applications of these methods in developing country contexts.
I happened to attend a session titled ‘ Big data for development: promises and perils’ that offered a lot of food for thought on privacy, confidentiality, digital rights, and data depository. Two fascinating points of discussion caught my attention. First, that the massive data available electronically in a myriad of forms provides a wealth of network of interactions. The field of computational social science is emerging to collect and analyze electronic data with an ‘unprecedented breadth and depth and scale’ and model economic and social interactions (see this article on Science here). This first point is first order and deserves its own space and attention.
The second point was made by Alex ‘Sandy’ Petland (the director of MIT’s Human Dynamics Laboratory and the MIT Media Lab Entrepreneurship Program among other things) who commented on the link between big data and inference. Paraphrasing the discussion: “With a large set of variables from different data sources, you generate lots of correlations. Some of these correlations might be the key to the missing key variables in a given context that small RCT studies with a limited number of controls might not provide (read omitted variable bias). You need to look at the structure of the data to make valid inferences’. This ‘big’ second question is the topic of this blog, spanning the debates already touched upon by this blog on external validity ( here), and the bigger questions of linking reduced forms to structural parameters.
How can we move beyond correlations in the presence of high dimensional data, and look for meaningful correlations and make valid inferences? A recent JEP paper by Belloni, Chernozhurov and Hansen reviews how the latest innovations in ‘data mining’ and how it links to causal inference and model selection. The paper follows and complements an outstanding mini-course online with the key recent econometrics developments, with publicly available videos and slides.
First of all what is big data? High dimensional data occurs when both ‘n’ (sample size) as well as ‘p’ (the number of available variables) are large.
The key objective of the empirical methods is to reduce this large dimension to a manageable set of variables (or what is referred to as ‘dimension reduction’). But how to parse the high dimensional forest and pick the important trees?
Prediction inference meets causal inference: both inferences share a common goal, reducing the dimensionality of high dimensional data to a manageable subset of variables with the objectives of 1) relating it to structural parameters of interest (causal inference) 2) making predictions (prediction inference).
Good data mining is a method that helps with this dimension reduction and model selection. The key for these specification searches is to find a rigorous method to do so. A popular method (LASSO) does so by minimizing squared errors, while putting a penalty on the size of the model (captured by the sum of absolute values of coefficients). LASSO and related methods are used to estimate these parsimonious models in an ‘approximately sparse’ way, that is by cutting irrelevant enough information while allowing some room for an approximation error. Potentially useful applications range from predicting regression functions to selecting instruments or controls.
What about causal inference? Take the problem of estimating treatment effects in partial linear models. Suppose to have your outcome equation:
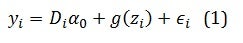
Where D the policy of interest, alpha is the impact.
The selection equation or auxiliary regression is given by:

where g(zi) and m(zi). and z is are the set of potential confounding factors (a linear function of controls xi or a polynomial transformation of xi). vi and Ei are error terms, (2) introduces the scope for omitted variable bias.
Belloni, Chernozhurov and Hansen propose a post double selection method:
- apply the parsimonious selection of controls in 1 by applying LASSO of y on D and x,
- apply the parsimonious selection of controls in 2 by applying LASSO of D on x,
- then estimate y on D and the union of the selected controls.
This blog just scratches the surface of this nascent and important literature. The authors have already provided extensions to more general models, such as heterogeneous treatment effects and quantile treatment effects.
Time to retool. And I look forward to reading applications of these methods in developing country contexts.


Join the Conversation