Many important policies are implemented at the national level. Monetary policy, fiscal policy, and many regulations are key examples. Pure time series or before-after analysis of the impacts of changes in these policies on the economy of a country will be contaminated by other changes going on in the economy. Simply trying to difference out global trends will not account for systematic differences in the growth path of the country where the reform took place from the average global growth path. This makes evaluation of the impacts of such policies difficult.
The Synthetic Control Method
The synthetic control method provides one approach for evaluating such policies. The method was introduced by Abadie and Gardeazabal in a 2003 AER paper, in which they try and assess the impact of terrorist conflict in the Basque country of Spain on per capita GDP in this region. The basic idea is as follows:
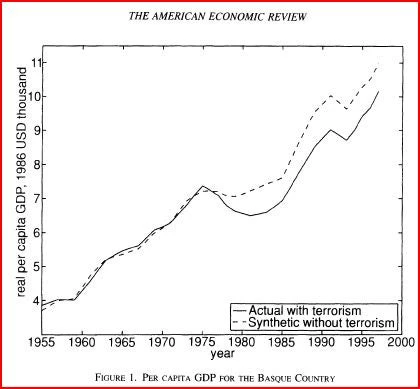
Step 1: Construct a “synthetic Basque region” as a weighted average of other regions of Spain, where the weights are chosen so the synthetic region most closely resembles the actual region before the intervention (terrorism here). Let X1 be a vector of pre-treatment economic variables for the treated region (Basque country), and X0 be the corresponding matrix of these variables for the J possible control regions. Then the weight matrix W is chosen to minimize (X1-X0W)’V(X1-X0W), where V is a diagonal matrix reflecting the relative importance of the different X’s. In their case this turns out to be a weighted average of Madrid and Catalonia, with zero weights on other regions.
Step 2: Calculate counterfactual outcome Y1*=Y0W, where Y0 is the outcome matrix for the control regions. Comparison of the counterfactual to the actual outcome provides the estimated treatment effect. This is shown in the figure below, which shows a fall in GDP once the terrorism starts.
Step 3: To assess statistical significance, perform this same method on every single control region, and then assess whether the measured impact of the reform is large relative to the effect one would estimate for a randomly chosen control region (where the intervention didn’t take place). This method is similar to small sample permutation testing, and was developed in Abadie et al. 2010, who applied the method to examine the impact of a tobacco-control program in California.
Applying it to Analysis of Country-Level reforms
Despite this method being around for a decade, I had not seen any applications to developing country data. A new paper by Gathani, Santini and Stoelinga is an exception. They suggest this method can be used to measure the impact of private sector reforms, such as the introduction of one-stop shops which make it simpler to start-up a business. They use the method to examine the impact of the introduction of a one-stop shop in Rwanda on new company registrations, and then go on to also apply the method to reforms in 11 other countries.
So what do they do?
They choose several macroeconomic variables to be X: GDP per capita, the shares of agriculture, industry and services in GDP, the trade balance, gross fixed capital formation as a percent of GDP, and the share of the population that is urban. They use this to form a “synthetic Rwanda” by finding a weighted average of other countries in terms of 2003-08 data (the reform occurred in 2009). They consider controls from 7 countries with GDP per capita below US$1000, which did not have a one-stop shop, and which had data on the outcome of interest (new firm registrations). This gives a potential control pool of Cambodia, Ethiopia, Indonesia, Moldova, Malawi, Pakistan and Uganda. Synthetic Rwanda turns out to be 0.405*Cambodia + 0.325*Malawi + 0.27*Ethiopia.
Synthetic Rwanda tracks actual Rwanda very well in terms of business registrations during the pre-reform period (2003-08), and then actual Rwanda shows a massive jump in business registrations once the reform is introduced (see Figure).
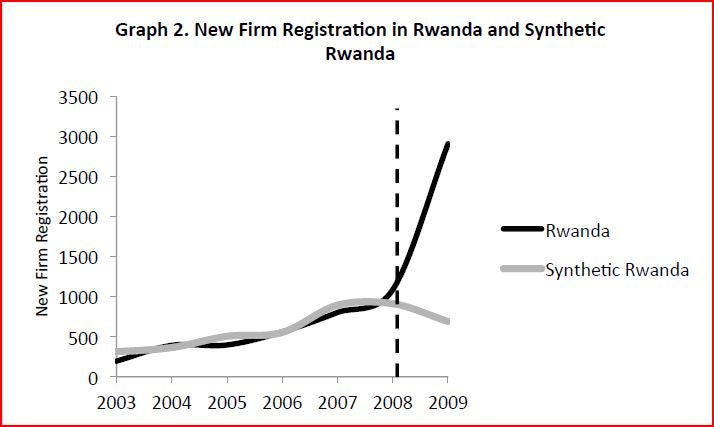
The authors then conclude that the reform led to an increase of 2,041 firms in 2009, an increase of 188%. This increase is much larger than they would find applying the same method to any of the seven potential control countries, leading them to conclude this is a genuine treatment effect.
Is this giving us a credible estimate of the reform impact, or what do we need to worry about?
This method is cheap to implement since it can be done with macro data; and it purports to give us the causal impact of national level reforms. So does the well-worn phrase “you can’t randomize monetary policy” not matter? Is this sort of method enough to make us confident of the impacts of reforms?
To my mind it is certainly a reasonable approach to take a first stab at a counterfactual. It is unclear how much better than before-after analysis it will be in many cases, but could be better in some cases – such as when there is a global recession or rapid technological advancement. Nonetheless, it is worth noting some caveats in applying this method:
· It will not work at isolating the impact of a particular reform if the country is reforming in a large number of areas at once. Countries like Rwanda, which have been high on the list of Doing Business top reformers, introduced a number of regulatory reforms all within a couple of years of each other – one would need to argue these other reforms have no impact on the outcome of interest. This is something the authors attempt to do.
· My gut-feeling is that the method is likely to work better for isolating the impact of reforms or events that take place in just one region within a country, using other regions in the same country to form a synthetic control region (as in the Basque and California examples) than when trying to isolate a country-level reform. This is because regions within a country share much of the same external shocks in terms of national government policy, exchange rate movements, inflation, etc. It seems to be more reasonable to think that if Madrid and Catalonia enter a recession, than so will the Basque country, than to think that Cambodia, Ethiopia and Malawi entering a recession will mean Rwanda does.
· We typically have a lot less data available at the macro level, resulting in fewer potential controls, and less time to show performance is the same pre-treatment. Showing the synthetic control matches the actual region for 20-30 time periods beforehand makes it more believable as a control than showing it matches over 5 time periods. In particular, one would like to see that the synthetic control doesn’t just match the treated region in terms of pre-treatment levels, but also in terms of sensitivity to business cycle conditions etc.
Nevertheless, this seems like a useful tool to use more often, so long as some care is taken in considering these caveats when interpreting the results. The Gathani et al. paper therefore should be a useful how-to read for many people trying to measure the impact of national-level policy changes.


Join the Conversation