Millions of dollars are spent each year trying to improve the productivity of firms in Africa (and those in other developing countries), yet we have very little rigorous evidence as to what works. In a new working paper I look at whether it is even possible to learn whether such policies even work, and what can be done to make progress.
Small number of firms + Large heterogeneity = Not much power
Firm census data reveal that once one looks at SMEs and large firms, the entire populations of interest in many African countries are relatively small – approximately 1000 to 2000 firms with 10 or more workers, and only 100 to 200 with 100 or more workers. Moreover, the World Bank enterprise surveys data reveal these firms to be very heterogeneous in terms of firm performance: the average cross-sectional coefficient of variation in firm sales is 3 to 4. i.e. the standard deviation of sales for these firms is typically three to four times the mean.
A typical World Bank project designed to improve the productivity of these firms involves between 100 and 500 firms over the course of five years. Table 1 shows the power of a randomized experiment with 300 treated and 300 control firms to detect different outcomes of interest, under the wildly optimistic assumption of 100% compliance with the treatment.
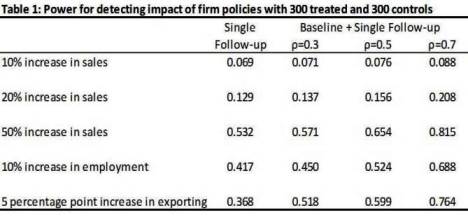
Typically one requires 80 to 90% power, whereas with a single follow-up survey one would only have 12.9% power to detect a 20% increase in sales, and 53.2% power to detect a 50% increase in sales. Increases of 10-20% in sales are often the targets set in developing such projects. As such, our power to detect whether a World Bank firm project meets its targeted goals is very low when such a single follow-up survey is done after the project is implemented.
Taking more rounds of surveys can help a bit – although how much depends on the autocorrelation of the outcome of interest (denoted ρ in the table). Typically for something like firm sales this autocorrelation is 0.5 or lower, in which case even a baseline and 4 rounds of follow-up surveys still only gives us 26% power for detecting a 20% sales increase.
What can be done?
The paper discusses several implications of these facts for designing firm experiments, and for what one can learn. The main ideas are:
· Focus on a smaller number of more homogeneous firms: there is little to gain and much to lose in terms of power by trying to look at an average effect in a sample that includes both lots of medium sized firms and a couple of really large ones – throw out the large firms.
· Collect a lot more data on these firms: Another recent paper of mine focuses on the role of repeated measurement in improving power. The gain in power from measuring the same noisy outcome at frequent intervals and averaging out noise can be large when outcomes are not that highly autocorrelated. With really large firms it may even be possible to get daily or weekly production data, as we do in a recent experiment on textile firms in India.
What does this mean for our efforts to learn about firm policies? The overall impact of some of our policies will be fundamentally unknowable without imposing additional structural assumptions. However, by collecting a lot more data and focusing on the largest, most homogeneous, subset of firms, experimental or non-experimental impact evaluations should have enough power to detect average impacts of the program for a large group of firms that matters.
This paper was the basis for my contribution to an interesting session last month at the Oxford CSAE conference entitled “Experiments or Structural Methods (or neither or both)? Video presentations are up here.


Join the Conversation