Note: I wrote this post almost two years ago, but it then got lost in our job market post season, and I forgot to publish it. I just came across it, and since I am still am not a fan of these leave-one-out instruments and still see them getting used, I thought I’d post it still with some small updates.
In a recent(ish) JPE paper, Fruehwirth et al. want to look at the impact of religion on depression in teens. That is, they would like to estimate an equation for person i like:
Mental Health(i) = a + b*Religiosity(i) + c’X + error
The concern is, of course, that religiosity is not random, and so we might worry about omitted variables (a shock like the death of a friend could cause people to become more religious and affect their mental health; socioeconomic backgrounds and home conditions may affect both religiosity and mental health) and reverse causality (maybe people stop going to church if they are depressed). The solution is to look for an instrumental variable. The authors use what is called a leave-one-out or spatial instrument. That is, they instrument person i’s religiosity with the average religiosity of person i’s peers, excluding i him or herself in this average, which we can denote Average Religiosity(-i). The first-stage is thus:
Religiosity(i) = c + d*Average Religiosity(-i) + d’X + error
They note that people can choose their peers, so look at variation in cohorts within schools, defining Average Religiosity (-i) on the basis of being in the same school-grade-race-gender-denomination group.
This type of instrument is used in a range of other settings too. For example, studies of the effect of democracy on growth instrument democracy with democracy in neighboring countries; these instruments have been used in a range of different political science papers; and I’ve seen them attempted in migration studies, where a household’s own migration is instrumented with characteristics of everyone else in their village.
What’s wrong with these instruments?
I’ve never been a fan of these instruments, and have written multiple referee reports over the years explaining why given applications have not been convincing. I was therefore very pleased to see discussion on twitter of a paper by Timm Betz, Scott Cook and Florian Hollenbach, published in 2018 in the journal Political Analysis, titled “On the use and abuse of spatial instruments”. In only 6 pages, it explains several issues with these types of instruments.
First, they note why people find these instruments appealing – they are convenient (you don’t need to collect other data, just use data you already have) and usually have a strong first-stage (the instrument relevance condition is often easily satisfied). Moreover, they note that we often have good theories why they should have a powerful first-stage – just as diffusion, competitive or peer effects, learning or other spillovers.
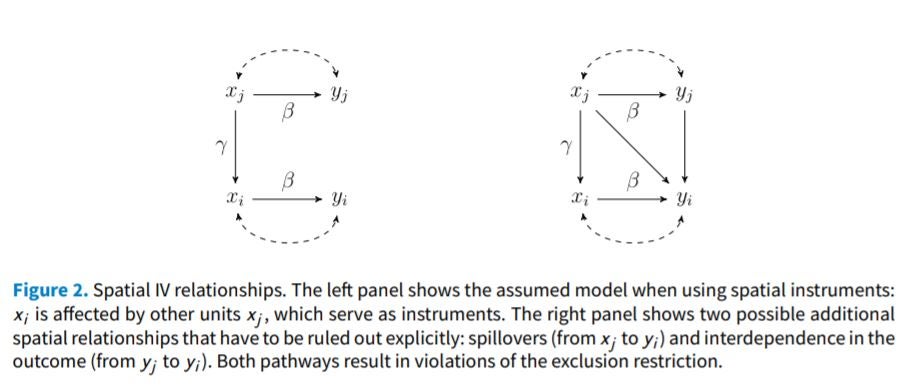
However, the problem is, of course, the exclusion restriction. They note two issues with satisfying the exclusion restriction. The first is that “spatial instruments require supporting the presence of one type of spatial relationship while concurrently denying other spatial relationships in the form of spillovers in predictors and interdependence in the outcome”. They illustrate this through this nice DAG below. Here x is the endogenous variable we want to instrument, and the left of the figure shows the assumptions needed – that x(j) (or x(-i) in my notation above) only affects y(i) through x(i) and not directly. The right panel illustrates two other plausible causal pathways that need to be ruled out: there can’t be direct spillovers (x(-i) can’t affect y(i)), or indirect impacts through interdependent outcomes (x(-i)->y(-i)->y(i)).
What does this mean in our opening religion example? We need to assume that the average religiosity of your peers affects your religiosity (believable – friends may discuss religion together, act as role models, etc.), but we need to rule out:
· x(-i) affecting y(i): the religiosity of my friends can only affect my mental health through my religiosity, and not directly. But maybe I get depressed that all my friends are celebrating some religious holiday and I’m not part of it, or I get annoyed when they protest certain dining choices, or my mental health is otherwise affected by them expressing their beliefs.
· x(-i)->y(-i)->y(i): any change in the mental health of my friends brought about by their religiosity can’t affect my mental health. But if my friends/classmates are now much happier, presumably this directly affects me.
Likewise Betz et al. give examples of why these assumptions are likely to be violated in most political science applications, due to spillovers and interdependences.
They note a second issue is that “spatial instruments produce simultaneity in the first stage and therefore are not exogenous—put simply, spatial instruments imply a first stage where left-hand side outcomes are included as right-hand side predictors”. In the first-stage equation example, Average religiosity of classmates is used as an instrument for i’s religiosity – but the religiosity of these classmates is in turn determined in part by i’s religiosity. Note that Sundquist (2021) discusses an exception to this concern in a recent working paper – in cases where there really is no simultaneity, but rather both x(i) and x(-i) are instead determined by a single unobserved variable z, which could be used as an instrument if it were observed – and so where x(-i) then serves as a proxy for z. Justifying this exception in practice will take a lot of work in convincing the reader in most settings.
As a result of these two problems, Betz et al. conclude “Jointly, these two problems imply that spatial instruments cannot be valid instruments. They do not even guarantee an improvement over OLS. We therefore advocate against the use of spatial instruments in their current form “. I totally agree, and am struck by the similarity to lagged instruments (remember the popularity of Arellano-Bond type dynamic panel instruments?), where the advantages of data availability and a strong first-stage were offset by lots of credibility of the exclusion restriction problems.
I should also note a third problem, which is the likely existence of other omitted variables, let’s call them u’s, that affect both x and y. The problem is that most applications do not have a story of why we should consider the variation in their instrument exogenous. E.g. there is no story of why the average religiosity of peers differs among similar people. It could be because they differ in socioeconomic background, or in where they live in the city, or other characteristics that affect both mental health and religiosity.
Finally, I should note that I am not trying to pick on the Fruehwirth et al. paper, which does a lot of robustness checks by adding different controls and examining different sub-samples to try and provide added support for their theory. Instead I’m pointing to the problem with this whole class of instrument, and re-iterating caution in using it.
post-script: thanks to Julian Reif on twitter for noting that Josh Angrist's 2014 Labour Economics paper "The perils of peer effects" discusses some related concerns.


Join the Conversation