The following two cases are quite common when reading/refereeing/trying to publish estimates of some effect size in an impact evaluation:
Case 1: the authors don’t have that large a sample, or have an outcome that is measured quite noisily, but they report large and significant treatment effects. The critical reader wonders whether the study was well-powered, so the authors take (or are asked to take) their estimated effect size and standard error, and ex-post calculate that power was really high.
Case 2: the authors don’t find a statistically significant result, and want to use this to argue that there is no treatment effect. But they then face questions about whether the study was well-powered, and are asked to do some ex-post power calculations with their data. For example, they might be asked to calculate the “observed power” where the observed treatment effects and variability are assumed to be equal to the true parameter values, and the probability of rejecting the null hypothesis of no effect is then computed.
In both cases, the use of estimated effect sizes to ex post calculate power is a bad idea and can give rise to very misleading results. Several papers have made this point over the years in other disciplines. For example, Hoenig and Heisey (2001) title their paper “The Abuse of Power: The Pervasive Fallacy of Power Calculations for Data Analysis”, and focus on case 2 above. Andrew Gelman has written extensively on case 1, and recently published a letter in the Annals of Surgery titled “Don’t calculate post-hoc power using observed estimate of effect size” (see also blogpost) in response to a suggestion that reporting guidelines in medical trials should require authors to disclose the power with the given sample size and effect size observed in a study.
Why are ex-post power calculations using observed effect sizes a bad idea? An illustration
To illustrate what can go wrong, we use some simulations where we know the true effect size, data generating process, and thus true ex-ante power. Consider a sample of 800 observations, divided equally into treatment and control. The outcome, Y, is given by:
Y = b*Treated + u, where u is i.i.d. N(0,1)
Consider first a true effect size of b=0.2 (i.e. 0.2 standard deviations). Then ex ante power is 80.7%. Since standard deviations are a problematic way of measuring effect sizes, we could interpret this effect size as capturing a 20% increase in income in a typical labor or firm intervention in which the mean is equal to the standard deviation, or capturing a 10 percentage point increase in a binary outcome like employment, when the control mean is 50%.
We then simulate 10,000 such experiments, each time getting the estimated effect size, the estimated standard deviation, and using both of these, calculate the ex-post power using this effect size. Figure 1 plots the resulting estimated ex-post power against the estimated effect size. Note first that although the mean and median estimated effect is 0.2, we get estimates of b ranges from -0.04 to +0.47, with a standard deviation of 0.07. If we happen to run one of the experiments where we get a statistically insignificant effect, we estimate b to be 0.1 on average, and would conclude the study is under-powered (the mean power is only 30% for the experiments with p>0.05). But otherwise, if we get a statistically significant effect, we end up overestimating the power of the study for detecting the true effect.
Figure 1: Ex-post power versus estimated effect size when true effect size is 0.2 and ex-ante power for this true effect size is 80%
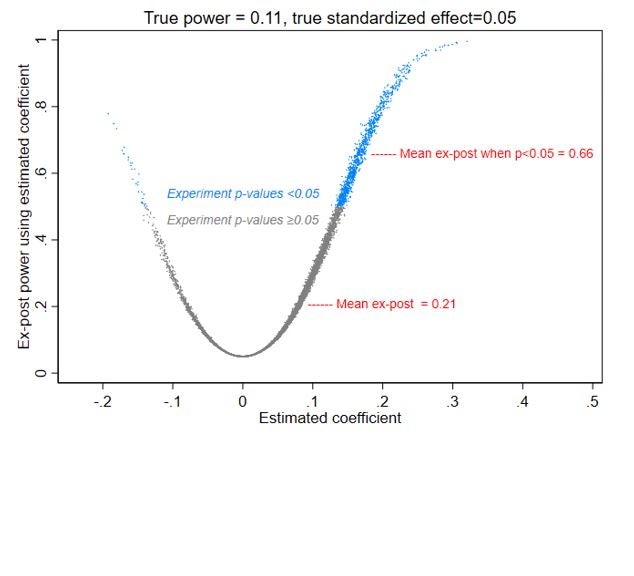
Now, let’s modify the above so that the true effect is actually 0.05 (e.g. only a 5% increase in income, or 2.5 percentage point increase in employment). The ex-ante power for this effect is only about 11%. That is, the experiment is now very low-powered for detecting the truth: it is unlikely to reject the null of no effect, even in the presence of the true effect.
Figure 2 plots the resulting estimated coefficients and the ex-post power using these estimated effect sizes. While the mean and median estimated b is 0.05, it ranges from -0.19 to +0.32. Note that if we find a statistically significant effect, the estimated treatment effect overstates the true magnitude (what Andrew Gelman calls a type-M error), and might even be the wrong sign (that thin wisp of blue dots on the left side of Figure 2 demonstrate what he calls type-S errors – see also this post). Moreover, an author could get an estimated impact of -0.19, and then report their study has ex-post power of 0.78, so claim you should trust their finding that this intervention has actually lowered employment or incomes.
Figure 2: Ex-post power versus estimated effect size when true effect size is 0.05 and ex-ante power for this true effect size is 11%
Why does this happen, and what should we do instead?
This happens because the estimated effect size is noisy, and it is precisely when it is noisy that we are most concerned about power – with large samples, little heterogeneity in the outcome amongst units apart from that due to treatment, and with precise measurements, we will get precise estimates of the treatment effect, and then ex-post power will be similar to ex-ante power using the true effect, and both will be high. That is, this so-called “ex-post power” is computed using two estimated quantities: the coefficient and the standard error. In the typical, only modestly-powered environment, the first of these is much more variable (in percentage terms – its distance to zero) than the second. And calculations that depend on two sources of nearly independent random variation are noisier than those that depend on just one such source.
A first approach is just not to report ex-post power at all, since it adds no additional information beyond what the p-value or confidence interval does – the observed ex-post power using the estimated treatment effect is a 1:1 function of the p-value or t-statistic. So non-significant p-values always correspond to low observed power.
But that may not be overly satisfactory, since we are often interested in whether an experiment was designed to have sufficient power to detect an interesting effect size in the first place. We know that ex-ante power calculations can be very crude – sample sizes in practice might change from those planned, the ex-ante calculations rely at best on baseline data and the mean and standard deviation of the control group may have changed dramatically by follow-up (this is particularly an issue for youth employment projects, where few are working at baseline), and the autocorrelations and intra-cluster correlations may be unknown in advance.
One solution is then to use the actual realized data from the control group to estimate ex-post the power for detecting an effect size that is interesting for theory or policy. This is what David did (with Chris Woodruff) in re-examining business training experiments and concluding they were mostly under-powered – he showed that using the actual sample sizes, control means, and control standard deviations, most studies had low power for detecting a 25% or even 50% increase in profits. Notice that these calculations use estimation regarding anticipated standard errors, but crucially they do not use any estimates of coefficients, just posited plausible coefficient values.
A second solution is to report the ex-post Minimal Detectable Effect (MDE), given your realized sample size and estimated standard error. Since this relies on the estimated, and not true (population, or expected), standard error, there will still be some variation from sample to sample. But this imprecision will be much less than with the ex-post power, and importantly, will be similar whether your point estimate of the treatment effect ends up being large or small, because it depends only on your (estimated) standard error, not your (more noisily estimated) treatment effect. Figure 3 illustrates this for the same simulations as in Figure 1 – we see that the estimated MDE clusters closely around the true MDE, and does not depend on whether the study found a significant result or not.
Figure 3: The Estimated MDE clusters closely around the true MDE
Now of course you can ask whether the MDE adds any additional information – after all, the MDE is just 2.8 times the standard error, so it is not telling you anything more than we already learn from seeing the standard error. But it can still be handy for comparing across studies, and making this transformation does make it easier to compare to what effect sizes are of interest given what we know from prior theory, expert opinion, etc. and to what size effects are needed for passing cost-benefit thresholds or otherwise attracting policy interest.
If you want to play around with this more yourself, all the code for running these simulations are available here in two parts (link 1, link 2).





Join the Conversation