 Suvarna in her fields with the ray of hope for Rain this yea
Suvarna in her fields with the ray of hope for Rain this yea
It has been nearly two decades since the publication by Elbers, Lanjouw, and Lanjouw, and their “ELL” method still remains one of the most applied poverty mapping approaches. Our new paper “Pull your small area estimates up by the bootstraps” delves into the history of the methods often used by the World Bank for poverty mapping and provides a methodological improvement to the institution’s toolkit. The new method yields estimates that are less biased and more precise. But before showing the results, we need to give a bit of background to poverty mapping and how it has been done within the institution.
Ever since the ELL method came out, the World Bank has assisted many client countries in its application, which has been largely simplified thanks to the PovMap software created by the institution. ELL is a method for small area estimation (SAE). SAE is an area of statistics that focuses on improving the precision of estimates in subpopulations when the corresponding survey data is not large enough to achieve a desired level of precision. Improved precision is achieved through models and use of census data. More precise estimates are of interest because these allow for better ranking of localities when designing territorial policies.
For statistical agencies, precision is of the utmost importance, thus, while poverty maps (such as those using machine learning and satellite imagery) have become popular, many of these poverty mapping techniques do not offer the precision that statistical agencies rely upon. Since ELL came out there have been considerable methodological advances; one that stands out is Molina and Rao (MR). MR introduced a new SAE approach, Empirical Bayes prediction (EBP), which conditions on the survey sample data available for areas of interest and thus makes more efficient use of the information at hand. Making use of the embedded assumptions of the model MR shows that EBP is superior to ELL since it produces more precise estimates.

Image: Donatas Dabravolkas/Shutterstock.com
In response to MR, Van der Weide provided a landmark update to PovMap and introduced a new approach based on EB prediction, here referred to as H3-CBEB, which incorporated survey weights to account for complex survey designs. Nevertheless, despite the addition of the new approach based on EB to the World Bank’s toolkit, considerable differences exist between the original EB approach of MR and that of Van der Weide.
The differences are linked to the computational methods used to obtain point and noise estimates under ELL and Van der Weide's update. The methods applied in PovMap take a cue from multiple imputation (MI). Under MI, the error is measured as the variance of all the simulated imputed values compared to the average of all the simulated imputed values. The parameters obtained from the survey model are not used to produce point estimates, instead these are used to draw parameters, which are then used to generate simulated vectors of welfare. Moreover, the objectives of MI are not aligned to the interests of SAE. Under SAE, methods that yield lower MSE are preferred whereas, under MI, the method that yields the lowest MSE yields invalid statistical inference.
Our paper corrects this issue by coupling the model fitting method presented in Van der Weide and ELL, to the simulation methodology of MR to produce poverty and noise estimates. The revised method uses a variant of EB called Census EB where the survey is not assumed to be a subset of the census. In our paper we show that the improvements are massive, not just yielding more precise estimates but also less biased estimates.
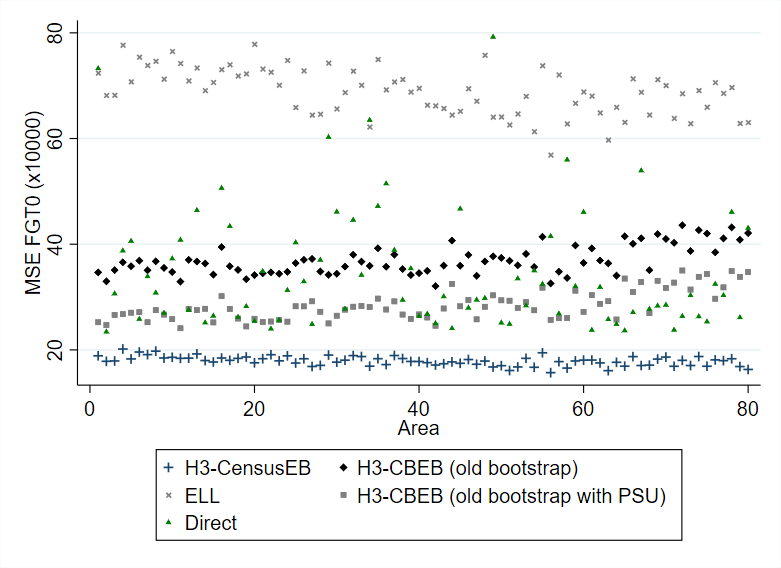
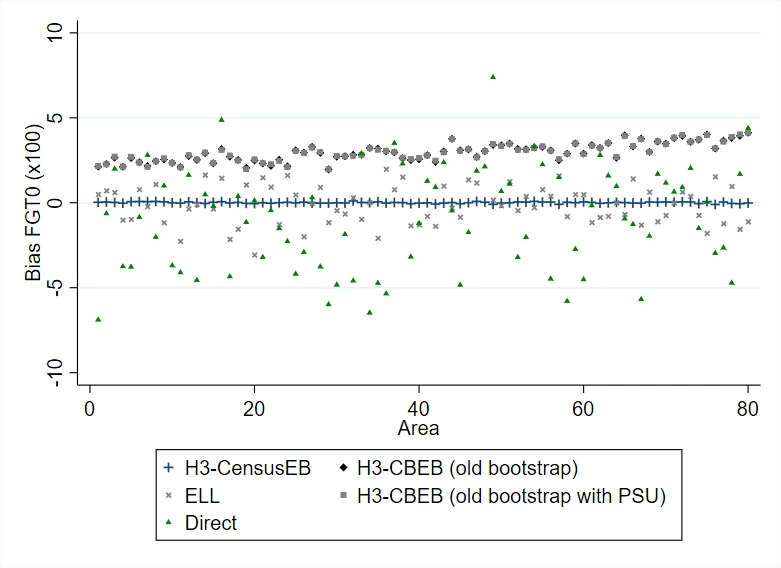
To show the improvements, in our paper we extend the simulation experiments of MR, by creating 10,000 different census populations using the assumptions of the modeling method. For each of these 10,000 census populations, a 20% sample is taken. The sample is used to obtain small area estimates of poverty for all areas in the population. The results show that MI-based methods are not appropriate for SAE. MI-based methods yield point estimates that are more biased and have a higher MSE. The bias in the case of H3-CBEB is quite considerable and mostly stems from the bootstrap procedure used to calculate the point estimates, based on taking cluster bootstrap samples. For each generated census, ELL also deviates considerably from the truth for any given area because it does not condition on the sample data as EB does. On the other hand, the updated H3-Census EB method shows minimal bias and a much lower MSE (Figure 1).
Figure 1: Bias and MSE of methods
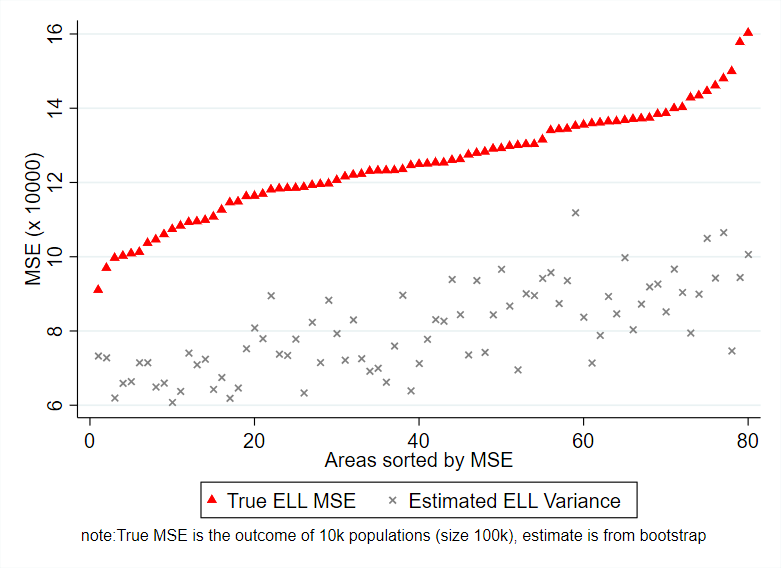
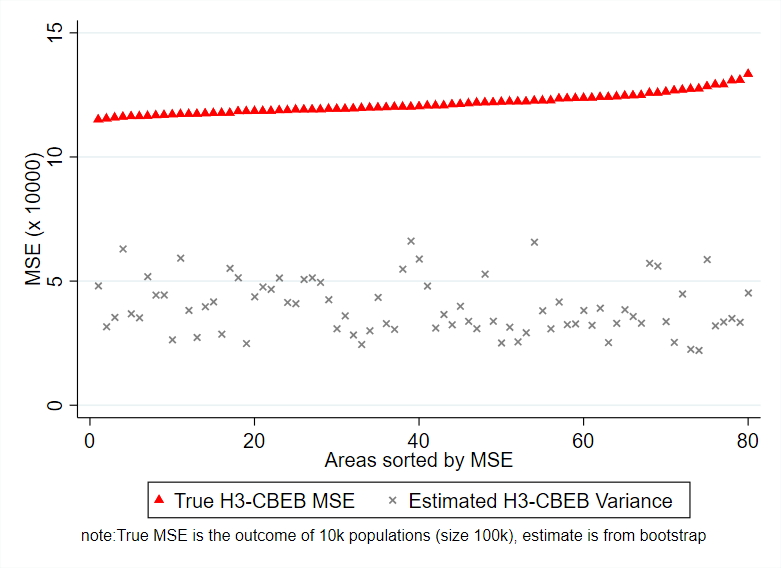
Another interesting finding is that although the true MSE from ELL and H3-CBEB is considerably higher than that of the updated method presented in our paper, the variance measure that has been used in PovMap, inspired in MI, underestimates the true MSE of the methods (Figure 2). This is a considerable improvement of the new methods since it allows for results that not only are more precise, but also more consistent.
Figure 2: True MSE and estimated variance of point estimates
All in all, the updated methods and toolkit should assist teams in producing poverty maps that are more aligned to the information at hand. To ensure World Bank teams take full advantage of our findings, the methods presented in the paper are now featured as an update to the Stata package produced by a team of researchers at the World Bank.




Join the Conversation