We are often in a world where we are allowed to randomly assign a treatment to assess its efficacy, but the number of subjects available for the study is small. This could be because the treatment (and its study) is very expensive – often the case in medical experiments – or because the condition we’re trying to treat is rare leaving us with two few subjects or because the units we’re trying to treat are like districts or hospitals, of which there are only so many in the country/region of interest. For example,
Jed wrote a
blog post about his evaluation of two alternative supply-chain management interventions to avoid drug stock-outs across 16 districts in Zambia, where he went with randomization and a back-up plan of pairwise matching. Were he exposed to the same problem today he might reconsider his options.
A new paper in the journal of Operations Research ( gated, ungated) by Bertsimas, Johnson, and Kallus argues that in such circumstances it is better to use optimization to assign units to treatment and control groups rather than randomization. Heresy? Not really: all you’re doing is creating groups that look as identical as possible using discrete linear optimization and then randomly assigning each group to a treatment arm, so you still get unbiased estimates of treatment effects while avoiding the chance of a large discrepancy in an important baseline characteristic between any of the two groups, giving your estimates more precision. And, according to the paper (theoretically and computationally), you do better than alternative methods such as pairwise matching and re-randomization.
The optimization minimizes the maximum distance (discrepancy) between any two groups for the centered mean and variance of a covariate. You get to choose how interested you are in the second moment with the choice of a parameter that can give it anywhere between no weight or equal weight and the model extends to using a vector of baseline characteristics and even higher order moments (skewness, kurtosis, etc.) but the model for optimizing the discrepancies in mean and variance is shown to do no worse than the other methods with respect to the higher order moments.
Under such optimization, treatment effects defined by the mean difference between two groups do not follow their traditional distributions, so you cannot do inference by using t-tests. Randomization inference (RI) is regularly used in small samples, Jed also wrote about this here, but in optimization subjects are not randomly assigned to the groups, so this is also not possible. But, there is a bootstrap method that is very similar to RI: simply redo your optimization (optimize to assign to groups, randomly assign groups to treatment, calculate treatment effect) over and over again while random sampling the study units with replacement. The p-value of your estimate is the percentage of times the actual treatment effect is lower than the bootstrapped treatment effect. In other words, if you’re able to generate a non-negligible number of larger effects just by randomly assigning the treatment group again and again in a bootstrapped sample, you should not be confident that the effect you found is due to the treatment rather than chance.
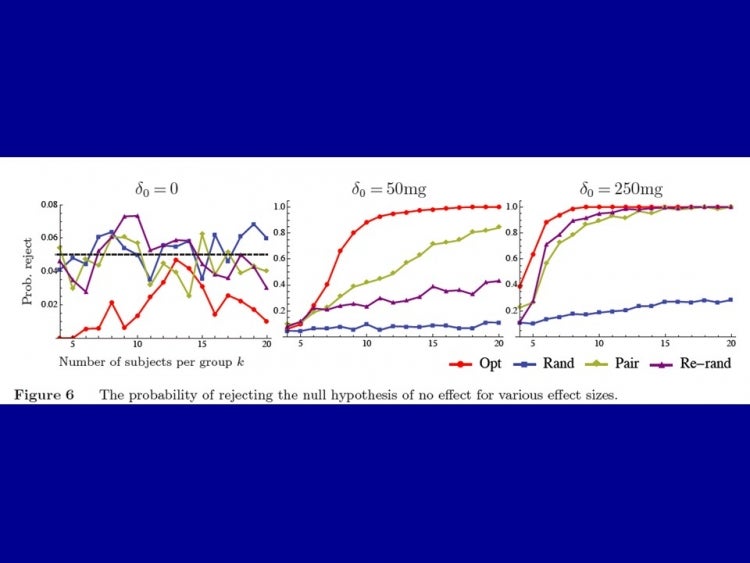
How does this affect power? The authors show that at certain levels of discrepancy between any two groups, say 0.1 standard deviations of the variable of interest, re-randomization and pairwise matching will come close to optimization, but for any smaller desired differences, they do exponentially worse. The power of the design is shown in the figure below for a hypothetical intervention that reduces the weight of tumors in mice by 0, 50mg, and 250mg. You can see, for example, that 80% power is reached with less than 10 mice per group in the optimization case, compared with about 20 in the best performing alternative (pairwise matching).
The authors suggest that the optimization routine is implementable on commonplace software like MS Excel or commercial mathematical optimization software and that the approach is a practical and desirable alternative to randomization for improving statistical power in many fields of study. If you give it a try (or have comments), let us know here and we’ll share…
A new paper in the journal of Operations Research ( gated, ungated) by Bertsimas, Johnson, and Kallus argues that in such circumstances it is better to use optimization to assign units to treatment and control groups rather than randomization. Heresy? Not really: all you’re doing is creating groups that look as identical as possible using discrete linear optimization and then randomly assigning each group to a treatment arm, so you still get unbiased estimates of treatment effects while avoiding the chance of a large discrepancy in an important baseline characteristic between any of the two groups, giving your estimates more precision. And, according to the paper (theoretically and computationally), you do better than alternative methods such as pairwise matching and re-randomization.
The optimization minimizes the maximum distance (discrepancy) between any two groups for the centered mean and variance of a covariate. You get to choose how interested you are in the second moment with the choice of a parameter that can give it anywhere between no weight or equal weight and the model extends to using a vector of baseline characteristics and even higher order moments (skewness, kurtosis, etc.) but the model for optimizing the discrepancies in mean and variance is shown to do no worse than the other methods with respect to the higher order moments.
Under such optimization, treatment effects defined by the mean difference between two groups do not follow their traditional distributions, so you cannot do inference by using t-tests. Randomization inference (RI) is regularly used in small samples, Jed also wrote about this here, but in optimization subjects are not randomly assigned to the groups, so this is also not possible. But, there is a bootstrap method that is very similar to RI: simply redo your optimization (optimize to assign to groups, randomly assign groups to treatment, calculate treatment effect) over and over again while random sampling the study units with replacement. The p-value of your estimate is the percentage of times the actual treatment effect is lower than the bootstrapped treatment effect. In other words, if you’re able to generate a non-negligible number of larger effects just by randomly assigning the treatment group again and again in a bootstrapped sample, you should not be confident that the effect you found is due to the treatment rather than chance.
How does this affect power? The authors show that at certain levels of discrepancy between any two groups, say 0.1 standard deviations of the variable of interest, re-randomization and pairwise matching will come close to optimization, but for any smaller desired differences, they do exponentially worse. The power of the design is shown in the figure below for a hypothetical intervention that reduces the weight of tumors in mice by 0, 50mg, and 250mg. You can see, for example, that 80% power is reached with less than 10 mice per group in the optimization case, compared with about 20 in the best performing alternative (pairwise matching).

The authors suggest that the optimization routine is implementable on commonplace software like MS Excel or commercial mathematical optimization software and that the approach is a practical and desirable alternative to randomization for improving statistical power in many fields of study. If you give it a try (or have comments), let us know here and we’ll share…


Join the Conversation