Does the intra-class correlation matter for power calculations if I am going to cluster my standard errors anyway?

This was a question posed by one of our readers in a comment on an earlier post I did on how to calculate the intra-class correlation in Stata. It was one of those questions that gnawed away at me for a while – intuitively I thought the answer was yes, but I could see where the reader was coming from – the whole idea of clustering the standard errors is to allow for an arbitrary correlation pattern within a cluster, so if I am allowing for this by clustering, maybe it doesn’t matter exactly what this pattern is.

So I finally got around to sitting down to spend more time thinking about this, and both considered the formula for the clustered standard error as well as ran some simulations in Stata. Turns out my original intuition was right – it does matter still. Here’s some rationale:

The theoretical reason

The variance of the clustered regression estimator is given by:

Where c is a degrees of freedom adjustment. At first glance it is not clear where the intra-class correlation enters. But it enters in the group average of the y, and also because we are estimating beta. Conditional on holding the total error variance constant, the higher the intra-class correlation, the less accurate is our estimate of beta. As a result, with high intra-class correlation, there will be much more variability in the u_g, resulting in larger standard errors.

I.e. while the cluster() option allows for arbitrary correlation within clusters, this correlation still does affect what the estimated standard error will be.

An empirical example

I generated a sample of 1000 observations in Stata, allocated into 50 clusters of 20 units each. I randomly allocated half the clusters to treatment, and then generated an outcome variable

Y = 5 + 0.5*treat + group-error + individual-error

I maintain the variance(group-error + individual-error) at 1, and then vary how much of the error is due to the group-level component and how much to the individual-component. I consider intra-class correlations of 0, 0.5, and 1. I then regress Y on treatment and save the estimated coefficient and the standard error calculated using the cluster command.

I do this 1000 times.

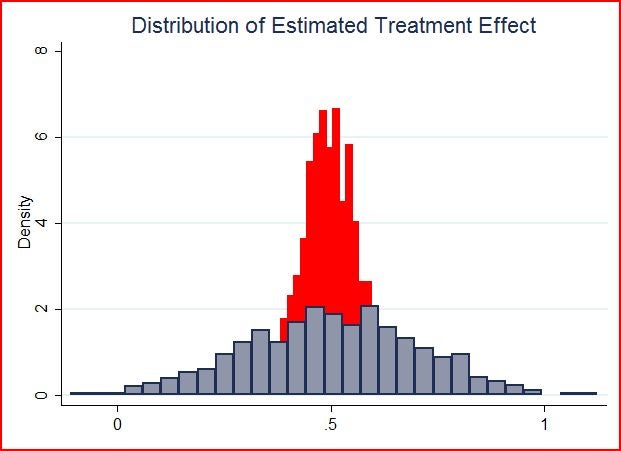
The graph below then shows the histogram of estimated treatment effect for an intra-cluster correlation of 0 (red) and 0.5 (light blue). Recall the true treatment effect is 0.5. You see that when the intra-cluster correlation is 0 (so we have 1000 independent observations), the estimated treatment effect is much more strongly concentrated around the truth than when there is correlation within clusters.

What does this then do to the standard errors obtained using the cluster command in Stata?

The histograms below show the distribution of the standard errors reported by Stata when the intra-cluster correlation is 0 (red), 0.5 (blue), and 1 (green). Note the variance of Y is 1 in all three cases, we have just varied how much of it is correlated within clusters. We see quite clearly how much smaller the standard error is when the intra-class correlation is lower.

So it does matter what this intra-class correlation is, even though you are planning on using the cluster command on any data you do collect.

Here is the Stata code for doing this, if you want to play around with it yourself.