I am writing to follow up on Berk’s post about using regression discontinuity design to evaluate the impacts of conditional cash transfer (CCT) programs. It happens that some colleagues and I at the International Food Policy Research Institute recently completed two papers using a unique regression discontinuity design (RDD) to evaluate the impacts of El Salvador’s Comunidades Solidarias Rurales (CSR) program. To evaluate the program, we came up with an innovative twist on RDD that we describe below.
CSR includes two types of transfers: an education transfer and a health transfer. Households are eligible for the education transfer if any members exist who are between 6 and 15 years of age and have not yet completed primary school; and for the health transfer if any pregnant women lived in the household at the time of the inception census or any children aged 0 to 5 years live in the household. The education transfer is conditional on school enrollment and attendance; the health transfer is conditional on growth monitoring check-ups, receiving timely vaccinations, and pre-natal monitoring check-ups for pregnant women. The transfer amount is $15 per month per household for either the education or the health transfer, and $20 per month if households are eligible for both types; it does not differentiate by the number of children in the household or affected by conditions.
In designing an impact evaluation for CSR, we were faced by several constraints. First, the program was already being implemented when we began the evaluation, and randomizing the remainder of the roll-out was not possible. So we knew that we would have to use a non-randomized evaluation methodology. Second, the roll-out of CSR was designed to first enroll the poorest municipalities, then gradually add relatively less poor municipalities. All of the municipalities in El Salvador were initially grouped into what were termed extreme poverty groups, and municipalities within the severe and high extreme poverty groups entered the program gradually between 2005 and 2009. Within each extreme poverty group, municipalities were ranked by a “marginality index” to determine the order of municipal entry into the program. The consequence is that we could use the roll-out to test for impacts using individuals in earlier entry groups at the “treatment” group with those in later entry groups as the control, but the sequential nature of municipality entry implied that difference-in-differences could not be used as an identification strategy alone, as initial trends might differ across groups, and we could not use matching methods, since variables existed that completely determine program eligibility. As a result, regression discontinuity design (RDD) remained as the only potentially valid design for identifying impacts.
So we knew we needed to use RDD, but we faced a further challenge. To measure impacts among the poorest municipalities possible (the 2006 entry group; the evaluation began too late to use the 2005 entry group), we had to compare treatment municipalities from the severe extreme poverty group entering in 2006 with control communities from the high extreme poverty group entering in 2007. The groups were formed using partitioned cluster analysis, which means that multiple variables were used to group municipalities into “like” groups—in this case, a poverty headcount and the severe stunting rate in first grade were used. So we needed to translate the use of partitioned cluster analysis into a single index with a threshold before we could apply RDD.
Dan Gilligan and I (link) show that by making three reasonable assumptions, the “distance” measure used to cluster observations in partitioned cluster analysis can be used as a forcing variable in RDD. The underlying concept is that each observation is assigned to a cluster, which is defined by its center. There are therefore a set of points that define a boundary between any two clusters equidistant from the two cluster centers, which becomes the RDD threshold. Our method is comparable to papers that either use a spatial boundary as an RDD threshold or the Papay et al. two-dimensional method (blog link here, gated paper here). However, our method is different from the former in that it is not limited to two dimensions; hypothetically, clustering could take place on several different variables. It differs from the latter that we break up space into two regions based on cluster analysis, rather than four regions.
We then use the estimator to show the impacts of CSR on age 6 through 12 school enrollment, which corresponds to kindergarten through 6th grade. In the paper, we estimate impacts using both the evaluation data we collected in collaboration with FUSADES in El Salvador and the national census data that were collected in 2007. Illustrating using the census data, we find that the program increased age 6 enrollment by about 19 percentage points between the 2006 and 2007 entry groups, where the distance to cluster threshold is the forcing variable (see graph below).
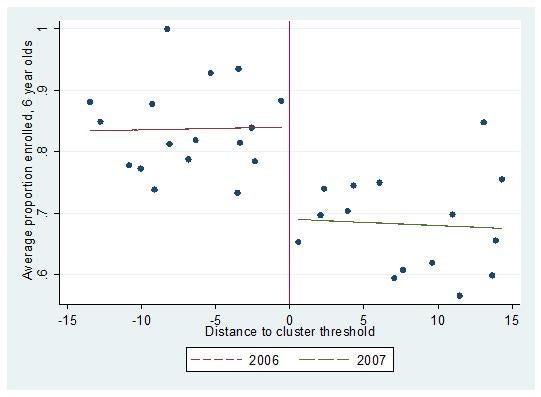
Average School Enrollment by Municipality, Children age 6, El Salvador Census, 2007
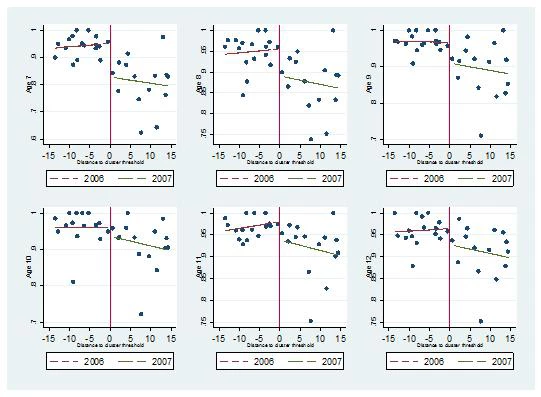
Among children of age to be in primary school (7 to 12 years old), the average impact on school enrollment is about 3.8 percentage points, regardless of the data source we use. With the census data, we are able to disaggregate into age-gender groups by year, and find larger impacts among younger children (age 7 and 8), no impacts among children aged 9 and 10, and small positive impacts among girls aged 11 and 12. We illustrate again below, by age. The important finding is that at least in poor communities, CSR appears to get children into school at younger ages, which should imply that children will be able to complete primary school in a more timely manner.
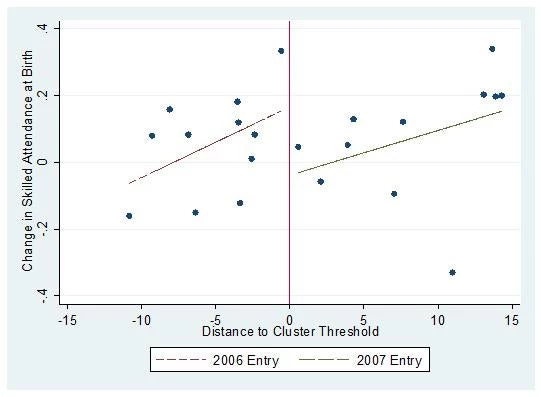
Amber Peterman and I use the same methodology to study four outcomes related to maternal health around the birth of children (link), using the IFPRI-FUSADES evaluation data. The four outcomes we study are whether women receive adequate pre-natal visits, whether qualified personnel attend their births, whether the birth takes place in a hospital, and whether or not they receive a post-natal checkup. Of these outcomes, cash transfers are only conditional on receiving pre-natal care, and even those are only conditional for women who were pregnant at the time of the census done by CSR officials to determine eligibility. We find robust impacts of CSR on skilled attendance at birth (illustrated below) and on birth in a hospital setting, but we find no impacts on pre-natal or post-natal care. The impacts are likely a result of a combination of supply side improvements and gains in women’s decision-making agency (the latter was a main conclusion of the qualitative study that accompanied our survey work). Perhaps more importantly for maternal health in El Salvador, after all municipalities in our data set entered CSR, women who were not eligible to be beneficiaries were just as likely as women who were in the treatment group to both have births attended by qualified personnel and for births to occur in hospitals. Therefore CSR appears to have catalyzed healthier outcomes in a longer term sense at the time of birth for women in poor municipalities in El Salvador.
Other than the results, which are important for policy makers in El Salvador, there is at least one further important implication from these papers. Even when an explicit forcing variable does not exist, it can be possible to measure the impacts of a CCT program (or another program). In fact, partitioned cluster analysis may be an attractive way for governments to target interventions to populations with specific needs—for example, it could be used to target areas for agricultural interventions with high poverty and high agricultural potential. Our method makes it possible to at least provide a local estimate of the impact of such a program, even if policy makers cannot be convinced to pilot the program through randomization.
Alan de Brauw is a Senior Research Fellow in the Markets, Trade, and Institutions Division at the International Food Policy Research Institute.

Join the Conversation