This is the eighth in our series of posts by PhD students on the job market
The low ratio of students from disadvantaged backgrounds going to college is a concern among academics and policymakers in many countries. In Latin America, for example, the gross enrollment rate in higher education from the poorest population quintile was 10% in 2018, more than 50% lower than among the wealthiest quintile. Different policies have been used worldwide to reduce this gap; one of the most popular and controversial is to give special consideration to specific groups’ college applications (known as affirmative action, quota, or positive discrimination). Such policies can be used in centralized and decentralized college admissions systems. However, affirmative action policies have distributional effects across different groups and the potential to create unintended pre-college reactions that affect the policy’s goal.
My job market paper investigates whether college admission policies based on students’ high schools incentivize students to switch schools and affect the policy's effectiveness in increasing access to college for disadvantaged students. The Chilean case is ideal for answering this question because the college application scores and the matching algorithm used in the system are transparent not only for researchers but also for applicants and universities. Furthermore, Chilean detailed administrative records for students during K-12 and college application allow researchers to simulate students' admissions under different policies.
The Chilean education system
Chile is among the least socially mobile countries in the world. The connection between school quality, student socioeconomic status (SES), and opportunities to attend college has been a key motivator for policy changes in Chile. Researchers have studied the Chilean education system and the different policies implemented to decrease inequality in access to quality K-12 and postsecondary education. These studies have shown that both the voucher system begun in 2008 for K-12 students and state-guaranteed loans introduced in 2006 have helped students from low-SES access better and higher levels of education (Neilson 2021, Solis 2017, Caceres-Delpiano et al. 2018).
These policies aside, reducing the gap between students from different socioeconomic backgrounds remains a work in progress. In 2011, for example, Chile experienced a prolonged strike from students demanding changes to the educational system, known as the Chilean Winter. The Relative Ranking policy I study in this paper is part of the policies implemented following this important social movement to increase equality in educational opportunities for all Chileans.
The relative ranking policy
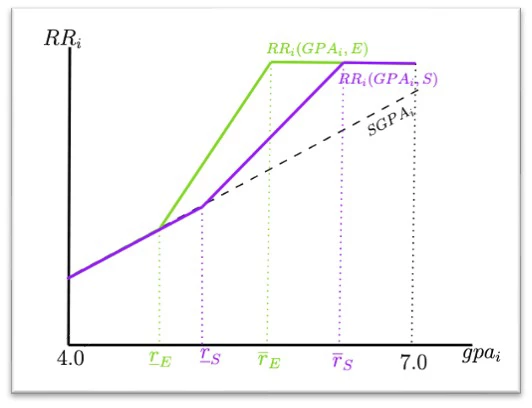
In Chile, all students who want to attend college must: (i) finish high school, (ii) take the national standardized test (PSU) offered once per year in December, and (iii) apply to up to ten preferred universities and major combinations. As a way to help students with high GPAs from low-quality schools, the “Consejo de Rectores de las Universidades Chilenas” (CRUNCH), the institution in charge of the centralized college admission system, decided to incorporate a new requirement: the students’ relative ranking (RR). The RR is computed such that if the student’s four-year GPA were below the mean of the three previous cohorts, they would receive the same score as the standardized GPA. If their GPA were above this mean but below the GPA of the best student among the three previous cohorts, their score would receive a boost. Finally, if the student had a four-year GPA higher than that of the best student among the three previous cohorts, they would receive the maximum points allowed for this component of their application. Why did CRUNCH use this comparison? In short, the CRUNCH did not want to create incentives for students to compete with their peers. This policy clearly could incentive other strategic behaviors, especially changing schools.
Figure 1 below presents two schools' ranking components with different RR formulas. We see that some students in school S would have a higher relative ranking if they graduated from school E because the GPA thresholds are lower. This difference represents an increase in a student’s application score simply for graduating from one school instead of another.
The effect on students’ high school choice
To evaluate whether the policy affected students’ likelihood of switching schools, I use several empirical techniques in my job market paper based on what students’ application scores would have been if they had graduated from a different high school than the one they attended for twelfth grade. I calculate these would-be application scores for students in different graduation cohorts by defining students’ choice sets, calculating the highest application score increase that a student would have had in their choice set (potential gain), and computing the potential score gain for every cohort, regardless of whether the RR policy was or was not in place. Then, using the potential gain, I estimate each student's likelihood of switching schools as a function of this variable. Using an event study design, I find that students with high potential score gains are, on average, 2.5 p.p. more likely to switch schools than students with no positive gain (baseline mean of 3.5 percent). Furthermore, the correlation between potential gain and probability of switching is positive only in the year of the policy, alleviating concerns about previous data trends. These seem to demonstrate that when students had full knowledge of how their RR would be calculated, switching schools was induced in order to receive a higher score. results
The effect of school switching on policy effectiveness
To estimate the effects of school switching decisions on policy effectiveness, I leverage the matching algorithm used in the centralized system and simulate three student degree allocations among the same pool of applicants. Figure 2 below presents the percentage change in enrollment for students from three socioeconomic groups for the top two most selective colleges. I simulate the pre-policy application score formula (base allocation), the revised application score formula based on all applicants’ beginning-of-the-year high schools (Benchmark), and the revised application score formula based on applicants’ graduating high schools (Real effect) and compute the change in the number of students accepted into college after the policy implementation with respect to the base allocation (Mover’s effect on policy).
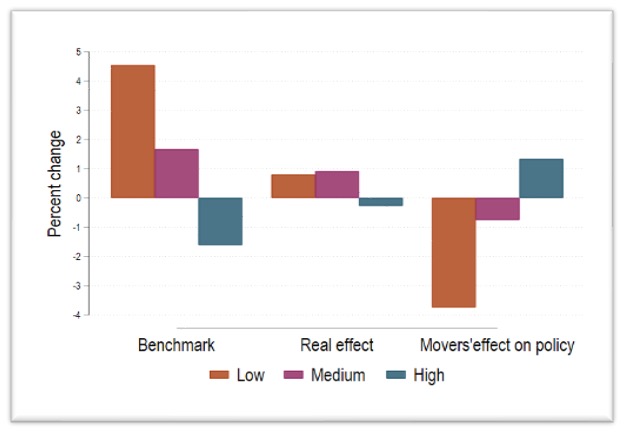
Although movers' effect on the total college acceptances is small (not shown), the results are bigger for the two most selective colleges (Figure 2). The number of low-income students accepted into the top colleges increased by less than 1 percent under the current policy. If students had not been allowed to switch high schools, that number would have increased by 5 percent, reducing the policy's effectiveness by 90 percent.
Policy implications
Many affirmative action policies trying to increase equal access to higher education have used schools to determine the policy’s beneficiaries. This strategy is compelling when we consider the connection between the type (public, voucher, and private) and the quality of schools that students from historically disadvantaged populations and communities attend. However, an important problem with these policies is the creation of incentives to game the policy among other students. My results suggest that switching high schools to increase one’s chances of getting into a top college is an one such strategy at play in policies that consider high school quality in an attempt to promote equity and accessibility in college admissions.
Carolina Concha-Arriagada is a Ph. D. Candidate at Georgetown University.


Join the Conversation