This is the 20th in this year’s series of posts by PhD students on the job market.
Competitive and undistorted markets allocate inputs efficiently across firms. Yet a large literature in macroeconomics and development argues that real-world markets fall short of this efficient benchmark, especially in developing countries. If markets do not work well, then capital may be stuck at firms with low returns, while other firms have high marginal products but are starved of capital.
In macroeconomics, prior work has found large losses in aggregate productivity from misallocation. This work has typically relied on strong assumptions about firm production functions (e.g. Cobb-Douglas) in order to measure marginal products. These papers thus conduct a joint test of allocative efficiency and auxiliary functional form assumptions. When that test rejects, it is not obvious if it is due to misallocation or misspecification.
A parallel literature in development microeconomics has found high and dispersed returns to capital, including in a variety of randomized controlled trials (RCTs). This is strong evidence against allocative efficiency, but it does not quantify the cost of misallocation.
In my job market paper (co-authored with David Hughes), we show how to bridge these two literatures, and measure misallocation with experiments. We first show that the cost of misallocation can be represented as a function of the variance of log returns to capital across firms. Next, we show how to use an RCT that gave grants to Sri Lankan microentrepreneurs (de Mel, McKenzie, and Woodruff 2008) to estimate the variance of returns to capital across firms. We also provide novel econometric tools to construct confidence intervals for this object. We find that optimally reallocating capital among the microenterprises we study would increase aggregate output by 22%.
Misallocation Is All About Dispersed Marginal Products
In efficient economies, the marginal product of capital is equalized across firms. Based on this logic, Banerjee and Duflo (2005) observe that the returns to capital vary substantially across firms in developing countries, and that this is evidence for misallocation of capital.
How do we quantify the cost of misallocation? Building on recent advances in the macroeconomics of aggregation (Baqaee and Farhi 2020), we provide a formula for misallocation that does not rely on any assumptions about firm production functions.
In partial equilibrium, the classic analysis of the cost of misallocation is the Harberger triangle, which measures the deadweight loss from a distortion. Figure 1 shows the (undistorted) supply and demand curves of an individual firm. The slope of demand depends on the elasticity of substitution across varieties, θ. The more easily consumers can substitute the firm's good with other goods, the more elastic demand. The firm's supply curve slopes up because as the firm grows larger, the marginal product of capital falls due to decreasing returns to scale (equivalently, marginal cost rises). The slope of supply depends on ϕ, the firm-specific elasticity of the MPK to output.
Figure 1: The Deadweight Loss from a Distortion
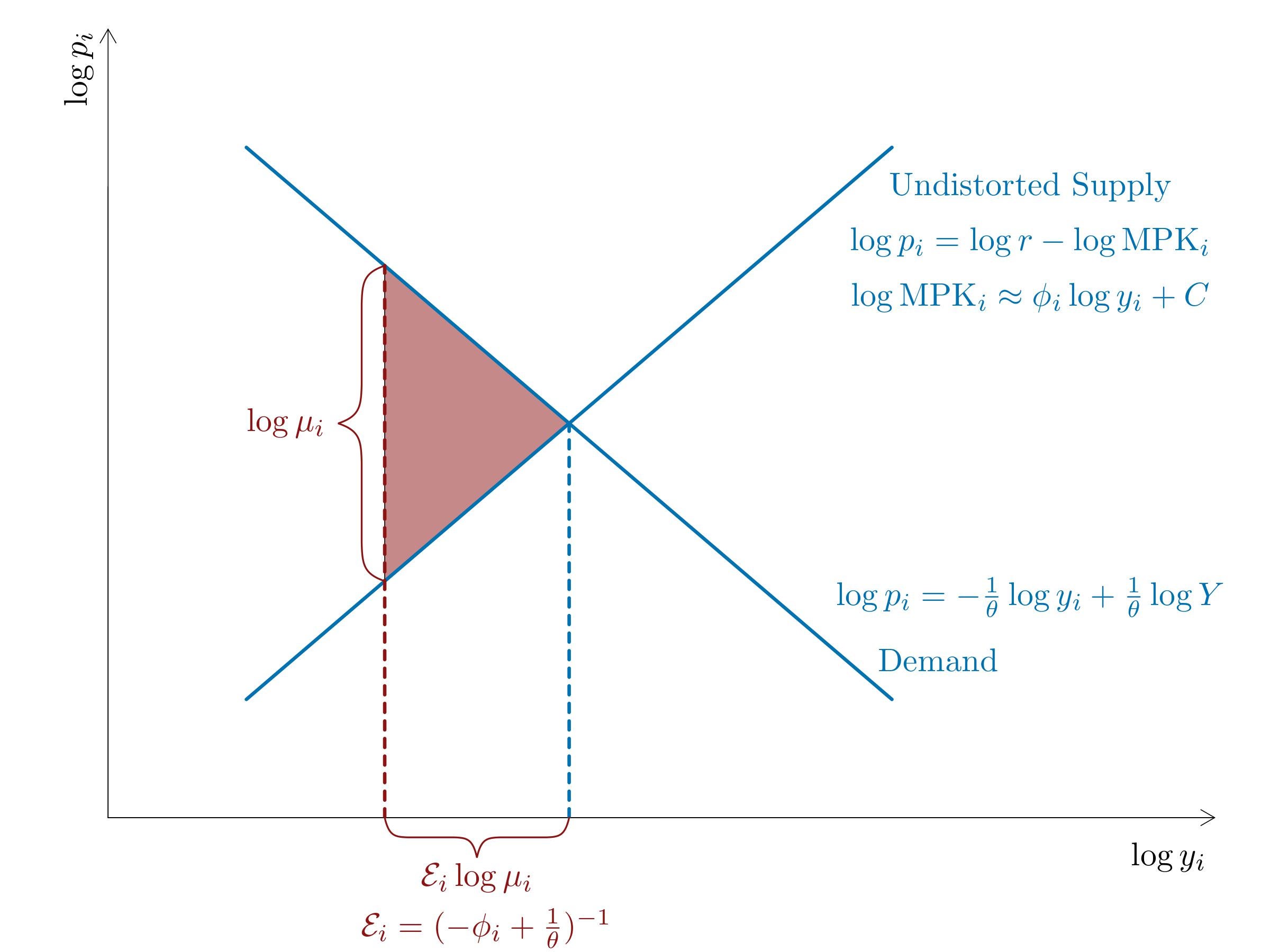
The firm faces some wedge, μ, which distorts the firm's first order condition. These wedges are a stand-in for all sorts of distortions, such as credit constraints, market power, or government policy. The wedge creates a deadweight loss, represented by the pink triangle. The size of that loss is the area of the triangle, which is one half the base (log μ) times the height of the triangle (ε·log μ), where ε is the elasticity of output with respect to the wedge. The elasticity ε is pinned down by the slopes of supply and demand, and will be higher when products are substitutable and returns to scale are high.
We show that in general equilibrium, the cost of misallocation is the sum of each firm’s Harberger triangle. However, misallocation only depends on the variance of log wedges, not the average wedge, since the cost of capital adjusts in equilibrium to make aggregate capital demand equal to supply. We show that if households are price takers and have CES demand, then the variance of log wedges is equal to the variance of the log marginal revenue product of capital. Simplifying, we get the following formula for misallocation:
Where Y is aggregate output and Y*is the efficient level of aggregate output. This formula is valid for arbitrary firm production functions and is accurate up to second order.
Measuring Heterogeneous Marginal Products Across Firms
To measure the variance of marginal products in the data, we turn to an experiment by de Mel, McKenzie, and Woodruff (2008). These authors randomized grants to Sri Lankan microenterprises, which they gave to fund investment in capital. They used these grants as an instrument for capital and estimate the average returns to capital. We are interested in not just the mean but the variance of returns to capital across firms.
We estimate heterogeneity in treatment effects by using covariates, measured at baseline, to predict heterogeneity in returns to capital across firms. We observe a range of variables at baseline, including the firm's pre-treatment capital, labor, and profits, the age of the business, and the owner's years of education. We include these covariates as interactions with capital, and use the grant received (interacted with covariates) as our instrument for capital. We also include firm and time fixed effects, as well as interacted fixed effects that allow for heterogeneous time trends by covariates. This yields the IV regression:
where kit is capital and Xi is a vector of baseline covariates. The variance of expected returns is given by Var(γ'Xi) = γ'Var(Xi)γ.
This regression identifies the variance of expected returns to capital, given baseline covariates. This in general will be a lower bound on the total variance. Our method comes with a few distinct advantages relative to the standard approach:
· Our method does not rely on any assumptions about the firm production function, aside from differentiability.
· Our method is robust to measurement error since it is based on an IV regression. In the standard approach, measurement error would show up as misallocation (Bils, Klenow, and Ruane 2021; Gollin and Udry 2021; Rotemberg and White 2021).
· Our method separates misallocation (differences in expected returns) from idiosyncratic risk (ex post differences in returns). Differences in returns that cannot be predicted ex ante are not evidence of misallocation: the world is stochastic, and some good bets do not pay off.
Our estimator of the variance of MRPK is a nonlinear function of the parameters from a heterogeneous linear IV model. In the paper, we show that standard methods to do inference on this object perform poorly, and we provide new econometric tools to construct valid confidence intervals.
Results
We find that there is substantial heterogeneity in returns to capital across firms, in the sample of Sri Lankan microenterprises that we study. Our preferred point estimates suggest a mean monthly return to capital of 8%, and a standard deviation of 9.8%, implying that the standard deviation of returns is 1.23 times the return. These estimates imply that a firm with returns one standard deviation below the mean is earning negative returns on capital. Our 90% confidence intervals rule out a standard deviation below 4% and a ratio below 0.47.
Using a standard calibration of ε (which we show in the paper is consistent with the data), we find that optimally reallocating capital across firms would increase aggregate output by 22%. For comparison, we show that the standard approach (Hsieh and Klenow 2009) would imply a potential gain of 34% from reallocating capital in our setting. Our results place the literature on misallocation on firmer footing, and show that there are sizable losses from misallocation of capital among microenterprises.
Jeremy Majerovitz graduated from MIT in 2022 and is a post-doc at the St. Louis Federal Reserve.


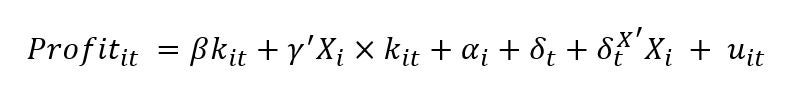

Join the Conversation