Be an Optimista, not a Randomista (when you have small samples)
This page in:
We are often in a world where we are allowed to randomly assign a treatment to assess its efficacy, but the number of subjects available for the study is small. This could be because the treatment (and its study) is very expensive – often the case in medical experiments – or because the condition we’re trying to treat is rare leaving us with two few subjects or because the units we’re trying to treat are like districts or hospitals, of which there are only so many in the country/region of interest. For example, Jed wrote a blog post about his evaluation of two alternative supply-chain management interventions to avoid drug stock-outs across 16 districts in Zambia, where he went with randomization and a back-up plan of pairwise matching. Were he exposed to the same problem today he might reconsider his options.
A new paper in the journal of Operations Research (gated, ungated) by Bertsimas, Johnson, and Kallus argues that in such circumstances it is better to use optimization to assign units to treatment and control groups rather than randomization. Heresy? Not really: all you’re doing is creating groups that look as identical as possible using discrete linear optimization and then randomly assigning each group to a treatment arm, so you still get unbiased estimates of treatment effects while avoiding the chance of a large discrepancy in an important baseline characteristic between any of the two groups, giving your estimates more precision. And, according to the paper (theoretically and computationally), you do better than alternative methods such as pairwise matching and re-randomization.
The optimization minimizes the maximum distance (discrepancy) between any two groups for the centered mean and variance of a covariate. You get to choose how interested you are in the second moment with the choice of a parameter that can give it anywhere between no weight or equal weight and the model extends to using a vector of baseline characteristics and even higher order moments (skewness, kurtosis, etc.) but the model for optimizing the discrepancies in mean and variance is shown to do no worse than the other methods with respect to the higher order moments.
Under such optimization, treatment effects defined by the mean difference between two groups do not follow their traditional distributions, so you cannot do inference by using t-tests. Randomization inference (RI) is regularly used in small samples, Jed also wrote about this here, but in optimization subjects are not randomly assigned to the groups, so this is also not possible. But, there is a bootstrap method that is very similar to RI: simply redo your optimization (optimize to assign to groups, randomly assign groups to treatment, calculate treatment effect) over and over again while random sampling the study units with replacement. The p-value of your estimate is the percentage of times the actual treatment effect is lower than the bootstrapped treatment effect. In other words, if you’re able to generate a non-negligible number of larger effects just by randomly assigning the treatment group again and again in a bootstrapped sample, you should not be confident that the effect you found is due to the treatment rather than chance.
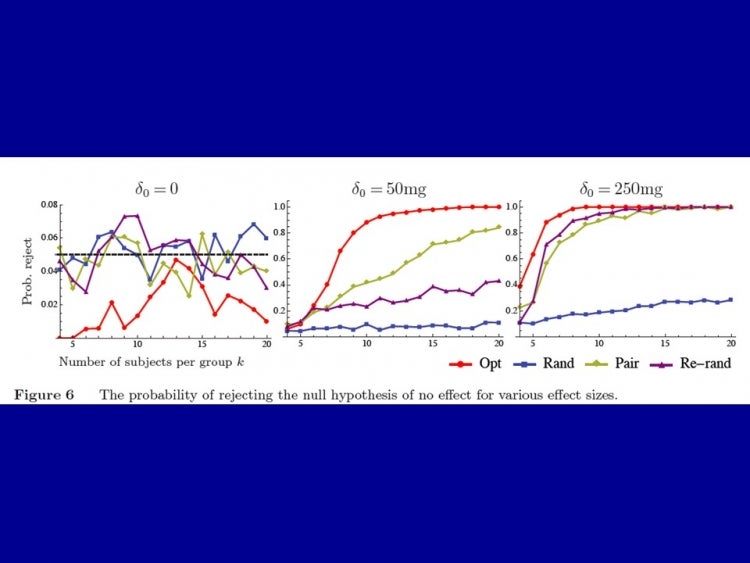
How does this affect power? The authors show that at certain levels of discrepancy between any two groups, say 0.1 standard deviations of the variable of interest, re-randomization and pairwise matching will come close to optimization, but for any smaller desired differences, they do exponentially worse. The power of the design is shown in the figure below for a hypothetical intervention that reduces the weight of tumors in mice by 0, 50mg, and 250mg. You can see, for example, that 80% power is reached with less than 10 mice per group in the optimization case, compared with about 20 in the best performing alternative (pairwise matching).
![]()
The authors suggest that the optimization routine is implementable on commonplace software like MS Excel or commercial mathematical optimization software and that the approach is a practical and desirable alternative to randomization for improving statistical power in many fields of study. If you give it a try (or have comments), let us know here and we’ll share…
A new paper in the journal of Operations Research (gated, ungated) by Bertsimas, Johnson, and Kallus argues that in such circumstances it is better to use optimization to assign units to treatment and control groups rather than randomization. Heresy? Not really: all you’re doing is creating groups that look as identical as possible using discrete linear optimization and then randomly assigning each group to a treatment arm, so you still get unbiased estimates of treatment effects while avoiding the chance of a large discrepancy in an important baseline characteristic between any of the two groups, giving your estimates more precision. And, according to the paper (theoretically and computationally), you do better than alternative methods such as pairwise matching and re-randomization.
The optimization minimizes the maximum distance (discrepancy) between any two groups for the centered mean and variance of a covariate. You get to choose how interested you are in the second moment with the choice of a parameter that can give it anywhere between no weight or equal weight and the model extends to using a vector of baseline characteristics and even higher order moments (skewness, kurtosis, etc.) but the model for optimizing the discrepancies in mean and variance is shown to do no worse than the other methods with respect to the higher order moments.
Under such optimization, treatment effects defined by the mean difference between two groups do not follow their traditional distributions, so you cannot do inference by using t-tests. Randomization inference (RI) is regularly used in small samples, Jed also wrote about this here, but in optimization subjects are not randomly assigned to the groups, so this is also not possible. But, there is a bootstrap method that is very similar to RI: simply redo your optimization (optimize to assign to groups, randomly assign groups to treatment, calculate treatment effect) over and over again while random sampling the study units with replacement. The p-value of your estimate is the percentage of times the actual treatment effect is lower than the bootstrapped treatment effect. In other words, if you’re able to generate a non-negligible number of larger effects just by randomly assigning the treatment group again and again in a bootstrapped sample, you should not be confident that the effect you found is due to the treatment rather than chance.
How does this affect power? The authors show that at certain levels of discrepancy between any two groups, say 0.1 standard deviations of the variable of interest, re-randomization and pairwise matching will come close to optimization, but for any smaller desired differences, they do exponentially worse. The power of the design is shown in the figure below for a hypothetical intervention that reduces the weight of tumors in mice by 0, 50mg, and 250mg. You can see, for example, that 80% power is reached with less than 10 mice per group in the optimization case, compared with about 20 in the best performing alternative (pairwise matching).
The authors suggest that the optimization routine is implementable on commonplace software like MS Excel or commercial mathematical optimization software and that the approach is a practical and desirable alternative to randomization for improving statistical power in many fields of study. If you give it a try (or have comments), let us know here and we’ll share…
I'm curious what you think about these optimization methods in comparison to minimum-maximum t-statistic randomization?
I could be wrong but isn't that what is called re-randomization in this paper? People mean two different things sometimes by it, one of which, I think, is the method to which you're referring...
Berk, you may also find this related paper by Max Kasy interesting. He also argues against using randomization when you have baseline data and want to minimize expected mean squared error. He finds that using the method he proposes leads to gains equivalent to increasing sample size by about 20%.
http://scholar.harvard.edu/kasy/publications/why-experimenters-should-n…
Hi Gautam,
Thanks -- David had also alerted me to that paper, which now I have to read along with the one Nathan cited above on arxiv.
This is a very interesting paper. However, one point to note is that it seems to assume an autocorrelation of 1 between baseline outcomes and follow-up outcomes when doing its simulation exercises. For many economic variables the autocorrelation is much lower, and so achieving such strong balance on baseline is no guarantee that balance will be as good at follow-up if there is no treatment effect - and so the power gains from baseline balance are much lower. My AEJ-Applied paper with Miriam Bruhn shows this for the case of pairwise matching and re-randomization, where the gains over pure randomization are much lower for outcomes like profits and consumption (low autocorrelation) than they are for test scores (high autocorrelation). I would think the same would be true for this method.
Berk, thanks for a great blog post!
David, your comments are right on and turn out to apply to a very wide range of experimental designs called a priori balancing, i.e. those that try (if at all) to balance covariates ONLY before treatment and before randomization. I study optimality among these designs in another paper, Optimal A Priori Balance in the Design of Controlled Experiments accessible at http://arxiv.org/abs/1312.0531. It turns out that among such designs (which include complete randomization, our OR paper, and many other designs including all those mentioned by you and the blog post), if the multiple correlation (R^2) between outcomes and covariates is reduced, then all such designs get the same exact hit to their corresponding post-treatment estimation variance. In the limit, if there is no association, then no matter what a priori balancing you do, nothing is better than complete randomization. So, first, you are right that this behavior applies widely -- I prove it theoretically and demonstrate it empirically. Second, if one were to reduce R^2 then all methods would experience the same hit and therefore variance and power plots are simply to show how different methods address the part of the variance that covariates can reduce to begin with; the rest is a constant addition of noise across the board. Apart from this across the board noise, within the confines of what could ever be potentially reduced by balancing covariates, our OR paper provides a method that accelerates the balancing from logarithmic rates (like 1 over a power of n, e.g. 1/sqrt(n)) to linear (aka exponential) rates (like 1 over an exponent in n, e.g. 1/2^n).
Now, what is really interesting is that it turns out that even if R^2 is very high, without any partial knowledge about the structure of the association between outcomes and covariates, taking an adversarial nature that can act within the confines of what you don't know, complete randomization is the optimal design. Hence, there is no free lunch -- you can't hope to reduce variance better than complete randomization without knowing something about the problem. When you do know something, various designs come out as "optimal." For example, if you know the association is what's known as Lipschitz continuous, then pairwise matching is optimal! If you know the association is linear, then moment matching is optimal! Extending this, one can think about associations that live in functional spaces that are common in machine learning for general consistent learning -- the so-called universal reproducing kernel Hilbert spaces (RKHS). These leads to new and powerful nonparametric designs that seem to work well in practice.
From of my practical experience with applying these methods to real data, however, I've found that matching first and second moments is almost always the best combination of efficient (when you have fewer moments you can match them better) and sufficient (first moments only can cause problems when things aren't very exactly linear and adding second moments seems to almost always solve this problem to a practically sufficient degree). Hence, in our short OR paper, this is the method we focus on and recommend for all practical experiments involving small samples.