A couple of weeks ago, Berk
blogged about a new paper by Bertsimas, Johnson and Kallus which argues that instead of randomization, it can be superior for power to choose the best of all possible allocations of subjects to treatment and control, where best is defined in terms of minimizing discrepancies in the mean and variance of the two groups. Several commentators pointed us to a related paper by Max Kasy, which is provocatively titled “
Why experimenters should not randomize, and what they should do instead” – where he argues that instead of randomizing experimenters should choose the unique non-random treatment assignment which minimizes a Bayesian or minimax risk function.
Re-randomization redux?
This idea that you can and should be trying to do a lot better than pure randomization does in terms of baseline balance is an old one, and is the justification for stratification, pairwise matching, etc. But I am reminded most of a practice that once appeared to be somewhat common in development field experiments, but which has fallen out of favor. I am referring here to re-randomization, which my paper with Miriam Bruhn ( gated, ungated) describes as taking two main forms in practice:
Concerns and Drawbacks of re-randomization and optimization:
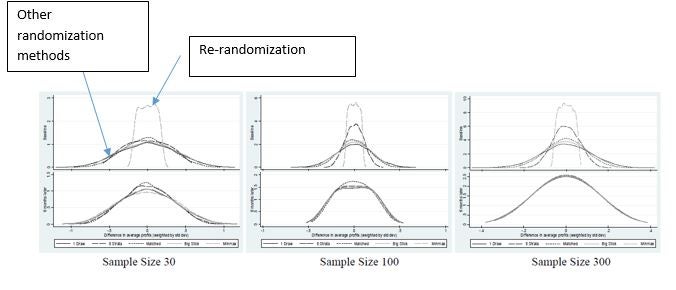
But then look at the lower panel, which shows what the difference in treatment-control profits are six months later (in the absence of any treatment effect) using the different methods. You can see that the re-randomization distribution does only slightly better than pure randomization for a sample size of 30, and as the sample size gets up to 300, you can not tell the different distributions apart. Basically when outcomes aren’t that correlated, getting balance on baseline doesn’t help much for follow-up balance.
2. You need to be extra careful about outliers. Consider a sample of 1 very rich person, 50 somewhat well off individuals, and 49 poor individuals. If you are trying to minimize the difference in means between two groups, the optimum can consist of putting the very rich person and all the poor individuals in one group, and all the somewhat well off in the other. That is, one outlier can lead you to favor an assignment that makes most people in one group not comparable with most people in the other group. You can of course try to deal with this through the objective functions you minimize, but unless you are careful, this can be a concern.
3. Inference is a pain: one of the benefits of running randomized experiments when it comes to analysis is that estimation and inference is typically relatively easy – just run a linear regression of the outcome on treatment, controlling for any stratification, and use the standard errors and t-stat on the treatment variable to test hypotheses about the treatment. In contrast, with re-randomization and optimization one cannot do this – you need to use bootstrapping with the Bertsimas et al paper, or perhaps permutation testing under the re-randomization restrictions. This is enough of a pain when it comes to estimating the main effect, but then if we want to also do things like examine treatment effect heterogeneity and interactions, get the TOT when take-up is imperfect, or other things which are relatively easy to do with regressions, we lose this machinery. This also becomes an issue once we think about how to deal with attrition and other real world phenomena affecting our data.
4. Finding the optimum isn’t currently doable on Stata – I know if it isn’t plug and play, then this makes it a lot more costly for people to use.
So when should you consider it
Bottom line is then I disagree with the title of Max’s paper. I don’t think it is worth trying to optimize in most circumstances. It is worth you looking into if you are planning an experiment that i) has a very tiny sample (more like the lab experiment samples or expensive drug piloting medical samples than most econ experiments); and ii) the outcome of interest is highly autocorrelated (so more useful for test scores and some health conditions than for profits, consumption or income). Otherwise I think I will continue to recommend randomization.
Re-randomization redux?
This idea that you can and should be trying to do a lot better than pure randomization does in terms of baseline balance is an old one, and is the justification for stratification, pairwise matching, etc. But I am reminded most of a practice that once appeared to be somewhat common in development field experiments, but which has fallen out of favor. I am referring here to re-randomization, which my paper with Miriam Bruhn ( gated, ungated) describes as taking two main forms in practice:
- The “big stick” method – whereby you do a random draw, check for balance, and if imbalance exceeds some specified threshold (e.g. t-stat>1.96), you take another draw.
- The minimum maximum t-stat method – where you take 1,000 or 10,000 random draws, and then for each draw, regress individual variable you want balance on against treatment, then choose the draw with the minimum maximum t-statistic.
Concerns and Drawbacks of re-randomization and optimization:
- The gains in power fall dramatically if outcomes aren’t highly correlated. The methods focus on getting the maximum possible balance on baseline variables. But balancing on balance variables only matters to the extent that these baseline variables strongly predict future outcomes. For many economic outcomes like consumption, profits, or income, the autocorrelation is often in the order of 0.3 to 0.5, and the gains from baseline balance are therefore very small. To see this, consider the figure below (taken from my paper with Miriam). This uses data on microenterprise profits from Sri Lanka. The top panel shows the distribution of the baseline treatment-control difference in average profits for many random draws using different randomization methods. The dashed line shows the minimum maximum t-statistic, which results in far fewer sizeable treatment control differences than other randomization methods. For optimization this would collapse to a single line at the minimum difference.

But then look at the lower panel, which shows what the difference in treatment-control profits are six months later (in the absence of any treatment effect) using the different methods. You can see that the re-randomization distribution does only slightly better than pure randomization for a sample size of 30, and as the sample size gets up to 300, you can not tell the different distributions apart. Basically when outcomes aren’t that correlated, getting balance on baseline doesn’t help much for follow-up balance.
2. You need to be extra careful about outliers. Consider a sample of 1 very rich person, 50 somewhat well off individuals, and 49 poor individuals. If you are trying to minimize the difference in means between two groups, the optimum can consist of putting the very rich person and all the poor individuals in one group, and all the somewhat well off in the other. That is, one outlier can lead you to favor an assignment that makes most people in one group not comparable with most people in the other group. You can of course try to deal with this through the objective functions you minimize, but unless you are careful, this can be a concern.
3. Inference is a pain: one of the benefits of running randomized experiments when it comes to analysis is that estimation and inference is typically relatively easy – just run a linear regression of the outcome on treatment, controlling for any stratification, and use the standard errors and t-stat on the treatment variable to test hypotheses about the treatment. In contrast, with re-randomization and optimization one cannot do this – you need to use bootstrapping with the Bertsimas et al paper, or perhaps permutation testing under the re-randomization restrictions. This is enough of a pain when it comes to estimating the main effect, but then if we want to also do things like examine treatment effect heterogeneity and interactions, get the TOT when take-up is imperfect, or other things which are relatively easy to do with regressions, we lose this machinery. This also becomes an issue once we think about how to deal with attrition and other real world phenomena affecting our data.
4. Finding the optimum isn’t currently doable on Stata – I know if it isn’t plug and play, then this makes it a lot more costly for people to use.
So when should you consider it
Bottom line is then I disagree with the title of Max’s paper. I don’t think it is worth trying to optimize in most circumstances. It is worth you looking into if you are planning an experiment that i) has a very tiny sample (more like the lab experiment samples or expensive drug piloting medical samples than most econ experiments); and ii) the outcome of interest is highly autocorrelated (so more useful for test scores and some health conditions than for profits, consumption or income). Otherwise I think I will continue to recommend randomization.


Join the Conversation