My colleague Bilal Zia recently released a working paper (joint with Emmanuel Hakizimfura and Douglas Randall) that reports on an experiment conducted with 200 Savings and Credit Cooperative Associations (SACCOs) in Rwanda. The experiment aimed to test two different approaches to decentralizing financial education delivery, and finds improvements are greater when Saccos get to choose which staff should be trained rather than when they are told to send the manager, a loan officer, and a board member.
One point of the paper that I thought might be of broader interest to our readers concerns the issue of what to do when you only have enough budget to survey a sample of a program’s beneficiaries, and you are concerned about getting enough compliers.
The problem
The experiment randomized 65 Saccos to get training where they could select who they send (autonomous selection), 65 Saccos to get training of specific people in the organization (fixed selection), and then 70 Saccos to be the control. Treated Saccos would then try to implement this training by training members.
Each of the Saccos has an average of 5,500 members. So the 130 treated Saccos have around 715,000 members, and the 70 control Saccos 385,000. The authors are interested in measuring outcomes at the member level, and have budget to survey 4,000 out of the 1,100,000 members, or 20 members per Sacco.
The authors were concerned that the take-up rate might be low for this financial education training offered by the Sacco, so were worried that if they just randomly sampled 20 out of the 5,500 members from a Sacco, by chance they could end up with very few people who had actually completed training. They did not have a baseline survey, and did not know the take-up rate until they went to the field for their first follow-up survey.
What did they do?
For both treatment and control Saccos, the authors got a roster of all community members. For the control Saccos they simply randomly chose 20 respondents to interview. For the treated Saccos, they matched these rosters to the attendance sheets for the financial education training sessions, and then, for each Sacco, randomly selected 10 trained members and 10 untrained members per Sacco. The actual attendance rate was 21-23%, so this meant they over-sampled compliers relative to non-compliers. In their analysis, they then weight the data using the probability of being selected.
Is this optimal?
The approach used by the authors will yield correct estimates, but does not maximize power. Let C(i) be the number of compliers in strata i, SC(i) the standard deviation of the outcome for compliers, N(i) be the number of non-compliers in strata i, SN(i) the standard deviation of the outcome for non-compliers, and n be the total number of units to be sampled from strata i. Then the optimal number of units to sample from the compliers is: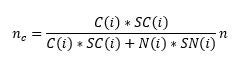
Now they do not know in advance the standard deviation of the outcomes, and so if we assume that the standard deviations are equal in the two groups, then this reduces to proportional allocation – i.e. if 23% of members in a Sacco took up financial education training, then 23% of the sample of 20, or 5 people, should come from the compliers, and the remaining 15 should be non-compliers. Proportional sampling within strata then has the advantage of making the overall sample self-weighting.
Note that in their case there is an additional level of sampling stratification, which is at the level of the Sacco. This will mean that the optimal proportion of the sample of 20 that should be compliers will then vary across Saccos – Saccos with higher take-up rates will have more trained members interviewed, while those with lower take-up rates will have fewer members interviewed.
So why might you want to oversample compliers?
The formula above suggests that the best thing to do is stratify on compliance, but then sample in proportion to the take-up rate. However, it does give one possible reason to oversample compliers – if you think the treatment will increase the variation in outcomes among those treated, then you will want to sample relatively more compliers.
In discussing this with Bilal, he mentioned a more practical reason: because they did not know the take-up rate in a community until they arrived at a Sacco, the field team had to match the attendance list to the Sacco roster, and then draw the sample. The simple rule of randomly choose 10 trained and 10 untrained to interview then involved much less enumerator calculation and possible discretion than having different sampling fractions in every community that had to be calculated on the spot.
Two other reasons you might want to oversample compliers can come about if compliance is really low:
- You might be interested in doing take-up regressions to help understand what characteristics are associated with take-up, and so want to make sure you have sufficient numbers of compliers to compare the non-compliers to.
- You might be concerned that take-up rates are so low that you may need to fall back on alternative non-experimental methods that focus on the impact on compliers, as in this other financial education evaluation.
- I’ve talked here about over-sampling compliers, but of course you may also want to over-sample non-compliers if take-up rates are very high and yet you want to say something about who doesn’t take up a program, or if non-compliance increases variance.
- Another example of over-sampling compliers comes up in the Miracle of Microfinance paper – they take a two-step procedure to deal with low take-up concerns. First, they conduct a census and identify characteristics associated with take-up. They then restrict their population of interest to a subset of households that have higher take-up – those who had lived in the area at least 3 years, and that had a women aged 18 to 55. They then note “Spandana borrowers identified in the census were oversampled because we believed that heterogeneity in treatment effects would introduce more variance in outcomes among Spandana borrowers than among nonborrowers, and that oversampling borrowers would therefore give higher power. The results ... weight the observation to account for this oversampling so that the results are representative of the population as a whole”. However, they do not report how much oversampling took place, or how they decided how much more variance they thought might occur.


Join the Conversation