After my last post on how to deal with missing values in baseline covariates in RCTs, a colleague wrote:
“I still haven’t seen a good discussion of whether you should do the demeaning and the interactions if your covariates are a whole bunch of strata (or even matched pair) dummies.”
So, I thought I’d do some research and write about that…
Let’s start with the basics:
If the strata dummies are the only covariates, then the following two methods are equivalent:
- Taking a weighted average of stratum-specific differences in means, with weights proportional to stratum size; and
- Regressing Y on treatment, the strata dummies, and the interactions of treatment with the de-meaned strata dummies (omitting one dummy to avoid collinearity)
DeclareDesign had a blog post a while back, to which we likely linked in Development Impact, which included some simulations related to this issue, among other things. Things go haywire with simply including block fixed effects (FE) when the share of treated varies substantially across blocks, which becomes a problem if there is treatment effect heterogeneity across blocks. This is less of an issue in the question I was asked: many blocked randomization (or matched pairs, quadruplets, etc.) designs have equal shares of treatment in each block/stratum by design.[1] In their simulations of horse racing a bunch of approaches, they show that the two methods above (blocked difference in means and the Lin approach) have no bias for the average treatment effect (ATE) and the smallest bias for the standard error (SE).[2] [3]
Is that the end of it? Not quite. What if you have some other covariates, you also would like to adjust for? If the number of your strata dummies is not very large and the number of units within each stratum is large enough, then the advice above still applies. But what happens when you have many strata with a small number of units within each stratum (say, you have matched quadruplets with two treated and two control units in each block)? In this case, you have a tradeoff because you will start running into degrees of freedom issues. [Needless to say, you cannot use the Lin approach with matched pairs...]
Here, it helps to think about why the block FE approach is advised (seemingly, as a rule) in the first place: because if you don’t use them, you’d be leaving money (precision) on the table. You blocked randomization with the covariates you used for a reason: most likely because they are prognostic of the outcome and so controlling for them achieves more precision. But suppose there's some other covariate that's strongly predictive of the outcome but wasn't used in the blocking. The gain from controlling for this covariate could be greater than the gain from controlling for the blocks. What should we consider then? Two ideas:
- If the probability of treatment varies by block, the analysis should still adjust for this (using either weighting or regression) to avoid bias.
- Beyond that, controlling for pre-specified covariates that are predictive of potential outcomes can help reduce the standard errors. Ideally, the blocking would have been based on the most strongly predictive covariates, so controlling for blocks is consistent with this advice. But if the blocking was unlucky or unwise, then controlling for the most strongly predictive covariates (if the approach is pre-specified) is more important than controlling for blocks.
[Usual disclaimer: Many thanks go to Winston Lin, who always has time to respond to my stats questions and who, at this point, should get his own byline in Development Impact. This post has benefited from several short exchanges with Winston over text messages. All errors are mine.]
[1] But, if you are interested in assessing heterogeneity across some other groups across which treatment assignment might be unbalanced, you’d be still exposed to this issue.
[2] There is a different way to think about the blocked FE approach, which is that it is a different estimand: it is a weighted ATE, where the weights are 

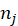 units are treated within block j, as described in the DeclareDesign blog. It’s what you have in your study population, and it might be OK for some people to prefer this estimand but be explicit about it (perhaps showing the treatment shares within blocks if they are unbalanced) …
units are treated within block j, as described in the DeclareDesign blog. It’s what you have in your study population, and it might be OK for some people to prefer this estimand but be explicit about it (perhaps showing the treatment shares within blocks if they are unbalanced) …
[3] If you want to dig deeper into this issue, here are some other resources: The “Taking block randomization into account section in Lin, Green, and Coppock (2016); Liu and Yang (2020); and Ma, Tu, & Liu (2020).


Join the Conversation