Just over a year ago, I wrote a blog post comparing different user-written Stata packages for conducting multiple hypothesis test corrections in Stata. Several of the authors of those packages have generously upgraded the commands to introduce more flexibility and cover more use cases, and so I thought I would provide an updated post that discusses the current versions. I’m also providing a sample dataset and do file that shows how I implemented the different commands. I again acknowledge my gratitude to the authors of these commands who have provided these public goods.
What is the problem we are trying to deal with here?
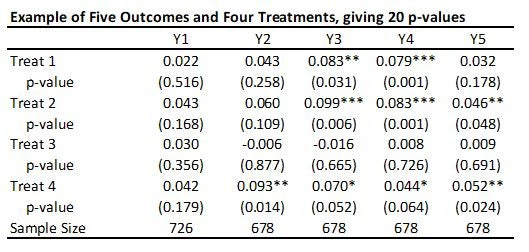
Suppose we have run an experiment with four treatments (treat1, treat2, treat3, treat4), and are interested in examining impacts on a range of outcomes (y1, y2, y3, y4, y5). In my empirical example here, the outcomes are firm survival (y1), and four different types of business practice indices (y2, y3, y4, and y5) and the treatments are different ways of helping firms learn new practices.
We run the following treatment regressions for outcome j:
Y(j) = a + b1*treat1+b2*treat2+b3*treat3+b4*treat4 + c1*y(j,0) + d’X + e(j)
Where here we have an Ancova specification, so control for the baseline value of the outcome variable in each regression y(j,0) – except for y1 (firm survival) since all firms were alive at time 0 and so there is no variation in the baseline value for this outcome; and control for randomization strata (the X’s here).
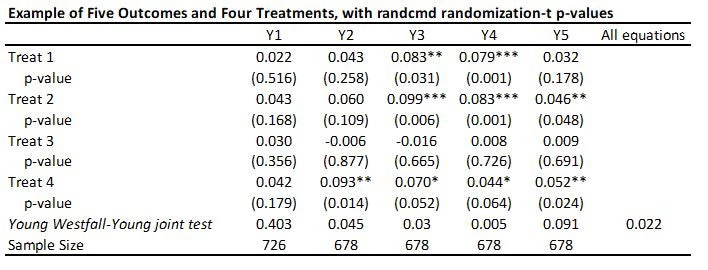
With 5 outcomes and 4 treatments, we have 20 hypothesis tests and thus 20 p-values, as shown in the table below:
Suppose that none of the treatments have any effect on any outcome (all null hypotheses are true), and that the outcomes are independent. Then if we just test the hypotheses one by one, then the probability that of one or more false rejections when using a critical value of 0.05 is 1-0.95^20 = 64% (and using a critical value of 0.10 is 88%. As a result, in order to reduce the likelihood of these false rejections, we want some way of adjusting for the fact that we are testing multiple hypotheses. That is what these different methods do.
Approaches for Controlling the False Discovery Rate (FDR): Anderson’s sharpened q-values
One of the most popular ways to deal with this issue is to use Michael Anderson’s code to compute sharpened False Discovery Rate (FDR) q-values. The FDR is the expected proportion of rejections that are type I errors (false rejections). Anderson discusses this procedure here.
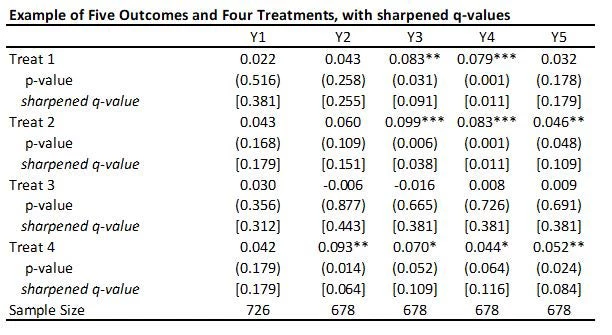
This code is very easy to use. You need to just save the p-values and then read them as data into Stata, and run his code to get the sharpened q-values. For my little example, they are shown in the table below.
A few points to note:
· A key reason for the popularity of this approach (in addition to its simplicity) is seen in the comparison of the original p-values to sharpened q-values. If we were to apply a Bonferroni adjustment, we would multiply the p-values by the number of outcomes (20) and then cap at 1.000. Then, for example, the p-value of 0.031 for outcome Y3 and treatment 1 would be adjusted to 0.62. Instead the sharpened q-value is 0.091. That is, this approach has a lot greater power than many other methods.
· Because this takes the p-values as inputs, you have a lot of flexibility into what goes into each treatment regression: for example, you can have some regressions with clustered errors and some without, some with controls and some without, etc.
· As Anderson notes in his code, sharpened q-values can actually be LESS than unadjusted p-values in some cases when many hypotheses are rejected, because if there are many true rejections, you can tolerate several false rejections too and still maintain the false discovery rate low. We see an example of this for outcome Y1 and treatment 1 here.
· A drawback of this method is that it does not account for any correlations among the p-values. For example, in my application, if a treatment improves business practices Y2, then we might think it is likely to have improved business practices Y3, Y4, and Y5. Anderson notes that in simulations the method seems to also work well with positively dependent p-values, but if the p-values have negative correlations, a more conservative approach is needed.
Approaches for Controlling the Familywise Error Rate (FWER)
An alternative to controlling the FDR is to control the familywise error rate (FWER), which is the probability of making any type I error. Many readers will be familiar with the Bonferroni correction noted above, which controls the FWER by adjusting the p-values by the number of tests. So if your p-value is 0.043, and you have done 20 tests, your adjusted p-value will be 20*0.043 = 0.86. As you can see, when the number of tests gets large, this correction can massively increase your p-values. Moreover, since it does not take account of any dependence among the outcomes, it can be way too conservative. All the methods I discuss here instead use a bootstrapping or re-sampling approach to incorporate information about the joint dependence structure of the different tests, thereby allowing p-values to be correlated and the adjusted p-values to be less conservative.
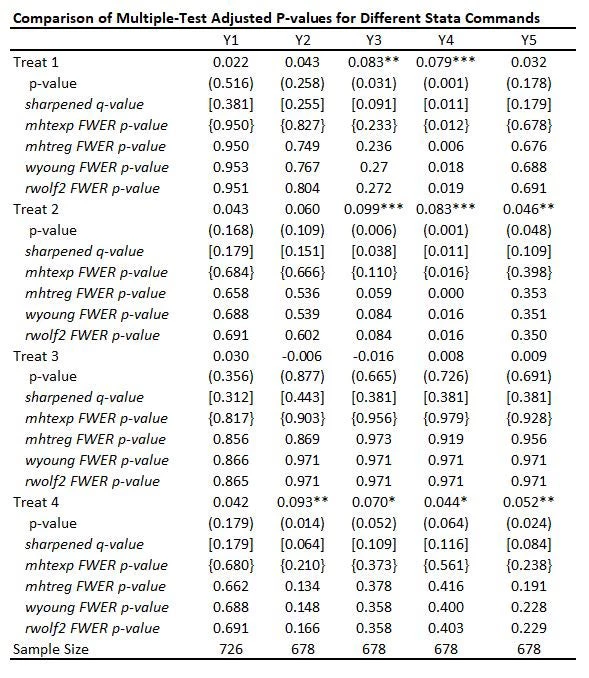
The table below adds FWER-adjusted p-values from four of these commands mhtexp, mhtreg, wyoung, and rwolf2, all based on 3,000 bootstrap replications. I discuss each of these commands in turn, but you will see that:
· All four methods give pretty similar adjusted p-values to one another here, with the small differences partly reflecting whether the method allows for different control variables to be used in each equation (discussed below).
· While not as large as Bonferroni p-values would be, you can see the adjusted p-values are much larger than the original p-values and also typically quite a bit larger than the sharpened q-values. This reflects the issue of using FWER with many comparisons – in order to avoid making any type I error, the adjustments become increasingly severe as you add more and more outcomes or treatments. That is, power becomes low. In contrast, the FDR approach is willing to accept some type I error in exchange for more power. Which is more suitable depends on how costly false rejections are versus power to examine particular effects.
Let me then discuss the specifics of each of these four commands:
mhtexp (and mhtexp2)
This code implements a procedure set out by John List, Azeem Shaikh and Yang Xu (2016), and can be obtained by typing ssc install mhtexp
List, Shaikh and Atom Vayalinka (2021) have an updated paper and code for mhtexp2 that builds in adjustment for baseline covariates using the Lin approach. It builds on work by Romano and Wolf, and uses a bootstrapping approach to incorporate information about the joint dependence structure of the different tests – that is, it allows for the p-values to be correlated.
· This command allows for multiple outcomes and multiple treatments, but mhtexp does not allow for the inclusion of control variables (so no controlling for baseline values of the outcome of interest, or for randomization strata fixed effects), and does not allow for clustering of standard errors. mhtexp2 does allow for the inclusion of control variables, but currently requires them to be the same for every equation, and still does not allow for clustering of standard errors.
· It assumes you are running simple treatment regressions, so does not allow for multiple testing adjustments coming from using e.g. ivreg, reghdfe, rdrobust, etc.
· The command is then straightforward. Here I have created a variable treatment which takes value 0 for the control group, 1 for treat 1, 2 for treat 2, 3 for treat 3, and 4 for treat 4. Then the command is:
mhtexp Y1 Y2 Y3 Y4 Y5, treatment(treatment) bootstrap(3000)
So note that my mhtexp p-values above are from treatment regressions that don’t incorporate randomization strata fixed effects or the baseline values of the control variables.
mhtreg
This code was written by Andreas Steinmayr to extend the mhtexp command to allow for the inclusion of different controls in different regressions, and for clustered randomization.
To get this: type
ssc install mhtreg
A couple of limitations to be aware of:
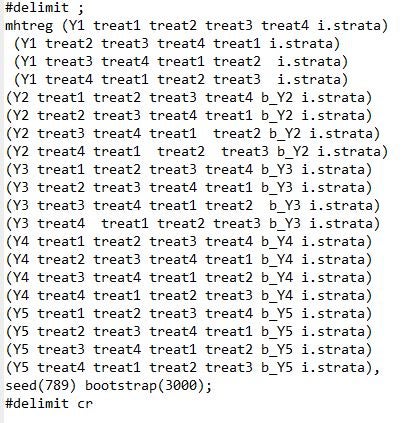
· The syntax is a bit awkward with multiple treatments – it only does corrections for the first regressor in each equation, so if you want to test for multiple treatments, you have to repeat the regression and change the order in which treatments are listed. E.g. to test the 20 different outcomes in my example, the code is:
· It requires each treatment regression to actually be a regression – that is, to have used the reg command, and not commands like areg or reghdfe; or for you to be doing ivreg or probits, or something else – so you will need to add any fixed effects as regressors, and better be doing ITT and not TOT or other non-regression estimation.
wyoung
This is one of the two commands that have improved the most since my first post, and it now does pretty much everything you would like it to do. This command, programmed by Julian Reif, calculates Westfall-Young stepdown adjusted p-values, which also control the FWER and allow for dependence amongst p-values. Documentation and latest updates are in the Github repository. It implements the Westfall-Young method, which uses bootstrap resampling to allow for dependence across outcomes. This method is a precursor to the Romano-Wolf procedure that the other three commands I note here are based on. Romano and Wolf note that the Westfall-Young procedure requires an additional assumption of subset pivotality, which can be violated in certain settings, and so the Romano-Wolf procedure is more general. For multiple test correction with OLS and experimental analysis, this assumption should hold fine, and as we see in my example, both methods give similar results here.
To get this command, type
net install wyoung, from("https://raw.githubusercontent.com/reifjulian/wyoung/master") replace
· A nice feature of this command is that it allows you to have different control variables in different equations. So you can control for the baseline variable of each outcome, for example. It also allows for clustered randomization and can do bootstrap re-sampling that accounts for both randomization strata and clustered assignment.
· The command allows for different Stata commands in different equations – so you could have one equation be estimated using IV, another using reghdfe, another with a regression discontinuity, etc
· The updates made now allow for multiple treatments and for a much cleaner syntax for including different control variables in different regressions. One point to note is that if there is an equation where you do not want to include a control, but you do want to include controls in others, the current command seems to require a hack where you just create a constant as the control variable for the equations where you do not want controls.
gen constant=1
#delimit ;
wyoung Y1 Y2 Y3 Y4 Y5, cmd(areg OUTCOMEVAR treat1 treat2 treat3 treat4 CONTROLVARS, r a(strata)) familyp(treat1 treat2 treat3 treat4) controls("constant" "b_Y2" "b_Y3" "b_Y4" "b_Y5") bootstraps(1000) seed(123);
#delimit cr
rwolf2
This command calculates Romano-Wolf stepdown adjusted p-values, which control the FWER and allows for dependence among p-values by bootstrap resampling. The original rwolf command was developed by Romano and Wolf along with Damian Clarke. It is the command that I think has improved the most with the recent update by Damian Clarke to rwolf2, described here. The updates expand the capabilities of the command to deal with what I saw as the main limitations of the original command, and it now allows for multiple treatments, different commands, different controls in different regressions, and also allows for clustered standard errors. Here is an example of the syntax:
Since this now does everything that the Westfall-Young command does, while been able to handle cases where subset pivotality does not hold, then this currently seems the theoretically best option for FWER correction at the moment.
Testing the null of complete irrelevance: randcmd
This is a Stata command written by Alwyn Young that calculates randomization inference p-values, based on his recent QJE paper. It is doing something different to the above approaches. Rather than adjusting each individual p-value for multiple testing, it conducts a joint test of the sharp hypothesis that no treatment has any effect, and then uses the Westfall-Young approach to test this across equations. So in my example, it tests that there is no effect of any treatment on outcome Y1 (p=0.403), Y2 (p=0.0.045) etc., and then also tests the null of complete irrelevance – that no treatment had no effect on any outcome (p=0.022 here). The command is very flexible in allowing for each equation to have different controls, different samples, having clustered standard errors, etc. But it is testing a different hypothesis than the other approaches above.
Putting it altogether
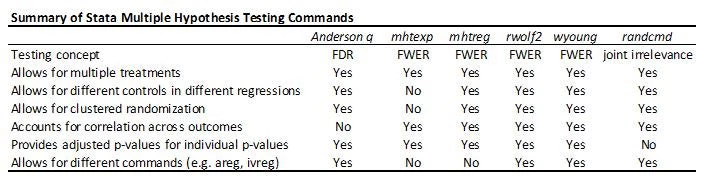
The table below summarizes the different multiple hypothesis testing commands. With a small number of hypothesis tests, controlling for the FWER is useful, and then both rwolf2 and wyoung do everything you need. With lots of outcomes and treatments, controlling for the FDR is likely to be preferred in many economics applications, and so the Anderson q-value approach is my stand-by. The Young omnibus test of overall significance is a useful compliment, but answers a different question.



Join the Conversation