Machine learning methods are increasingly applied in the development policy arena. Among many recent policy applications, machine learning has been used to predict poverty, soil properties, and conflicts.
In a recent Policy Research Working Paper by Paolo Brunori, Paul Hufe and Daniel Mahler (BHM hereafter), machine learning methods are utilized to measure a popular understanding of distributional injustice – the amount of unequal opportunities individuals face. Equality of opportunity is an influential political ideal since it combines two powerful principles: individual responsibility and equality. In a world with equal opportunities, all individuals have the same chances to attain social positions and valuable outcomes. They are free to choose how to behave and they are held responsible for the consequences of their choices.
A sizable number of empirical studies analyze the extent to which individuals have equal opportunities (Ferreira & Peragine, 2016). Often, these studies start by segmenting the population into a number of types, where a type is a group of individuals that are assumed to have the same opportunities. They may share, for example, the same gender, ethnicity or socioeconomic background. Next, the mean income of individuals belonging to a given type is used as a measure of the opportunities these individuals face. Individuals of types with a high average income come from a fortunate background with high chances of succeeding, and vice versa. Under this interpretation, inequality of opportunity can be calculated as the inequality in these type mean incomes. The more unequal the type incomes are, the more factors beyond individual control matter for determining individuals’ incomes.
To implement the approach above, one needs to specify what factors to use to segment the population into types. This choice is critical. If too few factors are considered, then the amount of inequality of opportunity will be underestimated. Consequently, inequality may be portrayed as arising dominantly from fair sources, leading inequality of opportunity to be a misleading policy construct. Conversely, if too many factors are considered when segmenting the population into types, part of the inequality that will be ascribed to factors beyond individual control will solely be due to sampling error, which does not reflect differences in opportunities.
The problem of how to measure individuals’ opportunities can benefit from a machine learning perspective. With the standard approach, the researcher must choose a specification that she thinks most adequately captures the emergence of unequal opportunities. In contrast, machine learning methods endogenize model selection. They can take all (measured) factors beyond individual control as inputs and use algorithms to segment the population into types. Hence, the model of how unequal opportunities come about is not a judgement call of the researcher but a non-arbitrary outcome of data analysis. Specifically, BHM suggest using conditional inference trees, which segment the population into types based on sequential hypothesis tests. Whenever two groups of individuals are claimed to have different opportunities, this is based on statistical tests rather than researcher intuition.
The following figure shows what the tree looks like for the case of Sweden:
Figure 1: Opportunity Tree in Sweden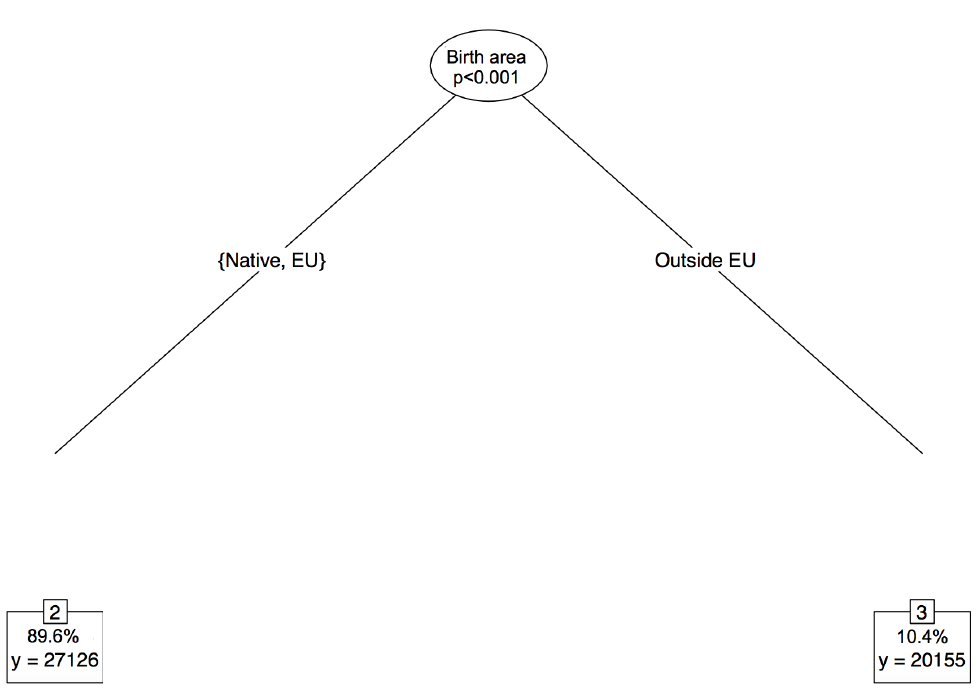
In Sweden, the population is only segmented into two types: individuals born outside of the EU (with an average annual equivalized household income of EUR 20,155), and individuals born in the EU (EUR 27,126). Within these two subgroups, we cannot reject that individuals face equal opportunities. This is a particularly low level of types compared with other countries. Consider for example the German tree, where many circumstances interact in determining a complex partition into types and a higher level of inequality of opportunity:
Figure 2: Opportunity Tree in Germany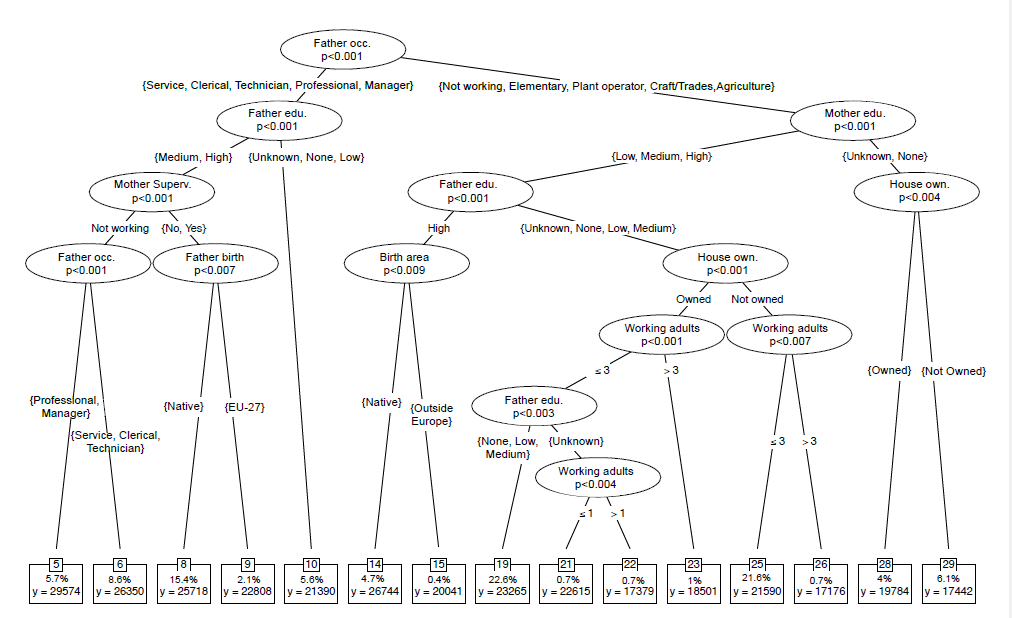
In addition to offering a data-driven segmentation into types, machine learning methods also yield more reliable estimates of individuals’ opportunities. This is particularly the case if we estimate a range of trees – obtaining what is known as a random forest – and use the income of the average type an individual belongs to as a prediction of his/her opportunities. These predicted incomes now serve as the measure of individuals’ opportunities since individuals with a high predicted income come from a fortunate background, and vice versa.
To illustrate the advantages of this method, inequality of opportunity is estimated in 31 European countries, and the ability of random forests to predict individuals’ incomes is compared to the standard approach. Both methods are applied to half of the dataset and the other half is used to assess how well the methods predict incomes out of sample.
Forests outperform the conventional approach in all 31 countries. In other words, forests capture inequalities more robustly due to factors beyond individual control, than the standard approach of the extant literature.
Why does this matter?
To ensure that prosperity is shared in a fair manner, we need to adopt policies that give people equal chances to succeed in life. This, in turn, requires precise and credible measures of the amount of inequality due to factors beyond individual control. Machine learning techniques offer a substantial advantage to that end.





Join the Conversation